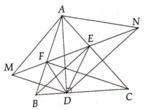
Cho tam giác ABC co ba góc nhọn. Kẻ đường cao AD. Gọi M, N lần lượt là các điểm đối xứng với D qua AB, AC. Đương thẳng MN cắt AB ở F, Cắt AC ở E. CMR: EB, FC, AD đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CH
Cô Hoàng Huyền
Admin
VIP
13 tháng 7 2016
Cô gợi ý nhé.
a. Nối AM, AN ta thấy tam giác AMN cân tại A. Từ đó suy ra đc AMN = ANM và suy ra FDA = ADE.
b. Cô làm cách này nhưng dùng kt lớp 9, em thử xem còn cách khác không nhé.
Góc FDA = ADE = ANE nên FAND là từ giác nội tiếp. Từ đó suy ra góc FAD = FND.
Vậy suy ra góc FAE = EDC = FDB = FMB hay tứ giác MAEB nội tiếp. Suy ra góc MAB = MEB. Mà MAB = FAD.
Vậy góc MEB = FND hay BE//DN. Vậy BE là đường cao. Tương tự CF cũng là đường cao nên AD, BE, CF đồng quy.

11 tháng 8 2019
a) Vì MD là trung trực AB trong ∆AMD
=> ∆AMD cân tại A
=> AM = AD
Vì DN là trung trực AC trong ∆ADN
=>∆ADN cân tại A
=> AD = AN
Mà AM = AD
=> AM = AN
=> ∆AMN cân tại A