Giải pt
\(\sqrt{ }\)2 sin3x-\(\sqrt{ }\)2cos2x=-1
tập nghiệm giải ra là x=π/36 + k2π/3 và x=17π/36 + k2π/3
bài này giải sao vậy ạ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 4 2017
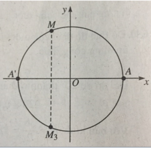
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
CM
20 tháng 1 2019
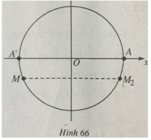
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
MA
1
HP
17 tháng 8 2021
\(4sin^2x.cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow2\left(1-cos2x\right).cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow2cosx-2cos2x.cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow2cosx-cos3x-cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow\sqrt{3}sin3x+cos3x=2cos2x\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin3x+\dfrac{1}{2}cos3x=cos2x\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{3}\right)=cos2x\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\pm2x+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{\pi}{15}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
L
1
5 tháng 9 2020
ngại viết quá hihi, mà hơi ngáo tí cái dạng này lm rồi mà cứ quên
bài trước mk bình luận bạn đọc chưa nhỉ
NQ
1
4 tháng 8 2019
ĐK:..........
Bình phương 2 vế ta được
\(2-3x+2\sqrt{\left(1-2x\right)\left(1-x\right)}=x+4\)
\(\Leftrightarrow2\sqrt{\left(1-2x\right)\left(1-x\right)}=4x+2\)
\(\Leftrightarrow\sqrt{\left(1-2x\right)\left(1-x\right)}=2x+1\)
\(\Leftrightarrow\left(1-2x\right)\left(1-x\right)=4x^2+4x+1\)
\(\Leftrightarrow1-3x+2x^2=4x^2+4x+1\)
\(\Leftrightarrow2x^2+7x=0\)
\(\Leftrightarrow x\left(2x+7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{-7}{2}\end{cases}}\)
Vậy.........................................
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2020
ĐKXĐ:...
\(\Leftrightarrow\frac{36}{\sqrt{x-2}}+4\sqrt{x-2}+\frac{4}{\sqrt{y-1}}+\sqrt{y-1}=28\)
Ta có:
\(VT\ge2\sqrt{\frac{36.4\sqrt{x-2}}{\sqrt{x-2}}}+2\sqrt{\frac{4\sqrt{y-1}}{\sqrt{y-1}}}=28\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\frac{9}{\sqrt{x-2}}=\sqrt{x-2}\\\frac{4}{\sqrt{y-1}}=\sqrt{y-1}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=11\\y=5\end{matrix}\right.\)
AK
1
PA
24 tháng 10 2017
Đặt \(\left\{{}\begin{matrix}\sqrt{x-2}=a\left(a>0\right)\\\sqrt{y-1}=b\left(b>0\right)\end{matrix}\right.\)
\(\Rightarrow\dfrac{36}{a}+\dfrac{4}{b}=28-4a-b\)
\(\Leftrightarrow\left(\dfrac{36}{a}+4a\right)+\left(\dfrac{4}{b}+b\right)=28\)
\(VT\ge2\sqrt{\dfrac{36}{a}\times4a}+2\sqrt{\dfrac{4}{b}\times b}=28\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\dfrac{36}{a}=4a\\\dfrac{4}{b}=b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\) \(\left(a,b>0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x-2}=3\\\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=11\\y=5\end{matrix}\right.\) (n)
Vậy . . . >3<