Vẽ đồ thị của các điểm, kết nối bằng một đường thẳng. Sau đó, kiểm tra hằng số tỷ lệ của bạn và viết phương trình.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gốc tọa độ lấy ở H. Gốc thời gian là lúc xe xuất phát từ H.
Công thức tính quãng đường đi của ô tô:
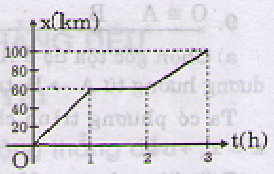
∗ Trên quãng đường H – D: S1 = 60t (x: km; t: h) với x ≤ 60 km tương ứng t ≤ 1 h.
∗ Trên quãng đường D – P: Do ô tô dừng lại 1h cộng với thời gian chuyển động từ H → D hết 1h nữa nên ô tô trễ 2h so với mốc thời gian đã chọn lúc xuất phát từ H. Ta có: S2 = 40.(t - 2) (km, h) với điều kiện t ≥ 2.
∗ Phương trình chuyển động của ô tô trên đoạn HD: x1 = 60t với x ≤ 60 km.
Trên đoạn D – P: x2 = 60 + 40(t - 2) với x ≥ 60 km, t ≥ 2h.
b) Đồ thị
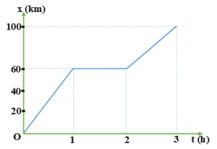
c) Trên đồ thị ta xác định được thời điểm xe đến P là 3h
d) Kiểm tra bàng phép tính:
Thời điểm ô tô đến P:
![]()

Vẽ đồ thị:
- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).
- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)
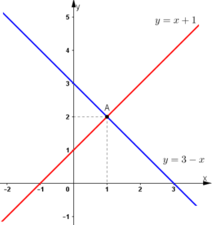
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).
Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).
Do đó phương trình f(x) = g(x) có nghiệm x = 1.
Kiểm tra bằng tính toán:
f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.
b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).
Kiểm tra bằng tính toán:
f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.
c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).
Kiểm tra bằng tính toán:
f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.

Chọn trục tọa độ Ox trùng với con đường H – P với O ≡ H, chiều dương H → P.
a)
. Đường đi của xe:
- Trên đoạn đường H – D: s = 60t (km,h) với s ≤ 60 km và t ≤ 1 h
- Trên đoạn đường D – P: s’ = 40(t – 2) (km,h); với t ≥ 2 h.
. Phương trình chuyển động của xe:
- Trên đoạn đường H – D: x = s = 60t với s ≤ 60 km và t ≤ 1 h
- Trên đoạn đường D – P: x = x0 + s
=> x = 60 + 40(t – 2) với s ≥ 60 km và t ≥ 2 h.
b) Đồ thị (hình vẽ)
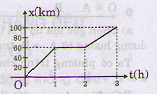
c) Xem đồ thị
d) Thời điểm xe đến P
t = + 1 +
= 3 h
Sau 3 giờ kể từ lúc xe xuất phát sẽ đến P.
Chọn trục tọa độ Ox trùng với con đường H – P với O ≡ H, chiều dương H → P.
a). Đường đi của xe:
- Trên đoạn đường H – D: s = 60t (km,h) với s ≤ 60 km và t ≤ 1 h
- Trên đoạn đường D – P: s' = 40(t – 2) (km,h); với t ≥ 2 h.
. Phương trình chuyển động của xe:
- Trên đoạn đường H – D: x = s = 60t với s ≤ 60 km và t ≤ 1 h
- Trên đoạn đường D – P: x = x0 + s
=> x = 60 + 40(t – 2) với s ≥ 60 km và t ≥ 2 h.
b) Đồ thị (hình vẽ)
c) Xem đồ thị
d) Thời điểm xe đến P:
t = + 1 +
= 3 h
Sau 3 giờ kể từ lúc xe xuất phát sẽ đến P.

b. PTHĐGĐ của hai hàm số:
\(x+2=-2x+1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)
Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)

\(b,\text{PT hoành độ giao điểm: }x+2=-2x+1\Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\Leftrightarrow y=\dfrac{5}{3}\Leftrightarrow A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\\ c,\text{Gọi }y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne1\\-\dfrac{1}{3}a+b=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{7}{3}\end{matrix}\right.\\ \Leftrightarrow y=2x+\dfrac{7}{3}\)