Khi một chiếc đĩa tròn quay đều thì một điểm trên vành đĩa chuyển động với vận tốc 3m/s. Một điểm nằm gần trục quay hơn một đoạn 10cm với vận tốc 2m/s. Xác định tần số, chu kì và gia tốc hướng tâm của một điểm nằm trên vành đĩa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)

Chọn đáp án D
+ Theo bài ra ta có f = 300 vòng/ phút = 5 vòng/s
+ Vậy tốc độ góc ![]()
+ Chu kỳ quay: T=1/f=0,2s
+ Vận tốc dài ![]()
+ Gia tốc hướng tâm:
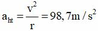

Tần số: \(f=5\)vòng/phút=\(\dfrac{1}{12}\)vòng/s
Chu kì chuyển động của vật: \(T=\dfrac{1}{f}=12s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{12}=\dfrac{\pi}{6}\)(rad/s)
Tốc độ dài: \(v=\omega\cdot R=\dfrac{\pi}{6}\cdot1=\dfrac{\pi}{6}\approx0,52\)(m/s)
Gia tốc hướng tâm: \(a_{ht}=\dfrac{v^2}{R}=\dfrac{\left(\dfrac{\pi}{3}\right)^2}{1}=\dfrac{\pi^2}{9}\approx1,1\)m/s2
\(f=\dfrac{n}{t}=\dfrac{5}{60}=\dfrac{1}{12}\left(\dfrac{vong}{s}\right)\)
\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{1}{12}}=12\left(s\right)\)
\(\omega=2\pi f=2\pi\dfrac{1}{12}=\dfrac{1}{6}\pi\)
\(v=\omega R=\dfrac{1}{6}\pi\cdot2=\dfrac{1}{3}\pi\)
\(a_{huongtam}=\dfrac{v}{R}=\dfrac{\left(\dfrac{1}{3}\pi\right)^2}{1}\approx1,1\left(\dfrac{m}{s^2}\right)\)

1 phút = 60s
- Chu kì: T = \(\dfrac{t}{n}\)= \(\dfrac{60}{4}\)= 15 (s)
- Tần số: f = \(\dfrac{1}{T}\)=\(\dfrac{1}{15}\)(Hz)
- Tốc độ góc: T = \(\dfrac{2\pi}{\omega}\) \(\Rightarrow\) \(\omega=\dfrac{2\pi}{T}\)\(=\) \(\dfrac{2\pi}{15}=\dfrac{2}{15}\pi\) (rad/s)
- Tốc độ dài: \(\upsilon=r\omega\) ⇔ \(\upsilon=\dfrac{3}{2}.\dfrac{2}{15}\pi\) = \(\dfrac{1}{5}\pi\) (m/s)
- Gia tốc hướng tâm: \(a_{ht}=r.\omega^2\Leftrightarrow a_{ht}=\dfrac{3}{2}.\left(\dfrac{2}{15}\pi\right)^2\)\(\simeq\) 0,263 (m/\(s^2\))


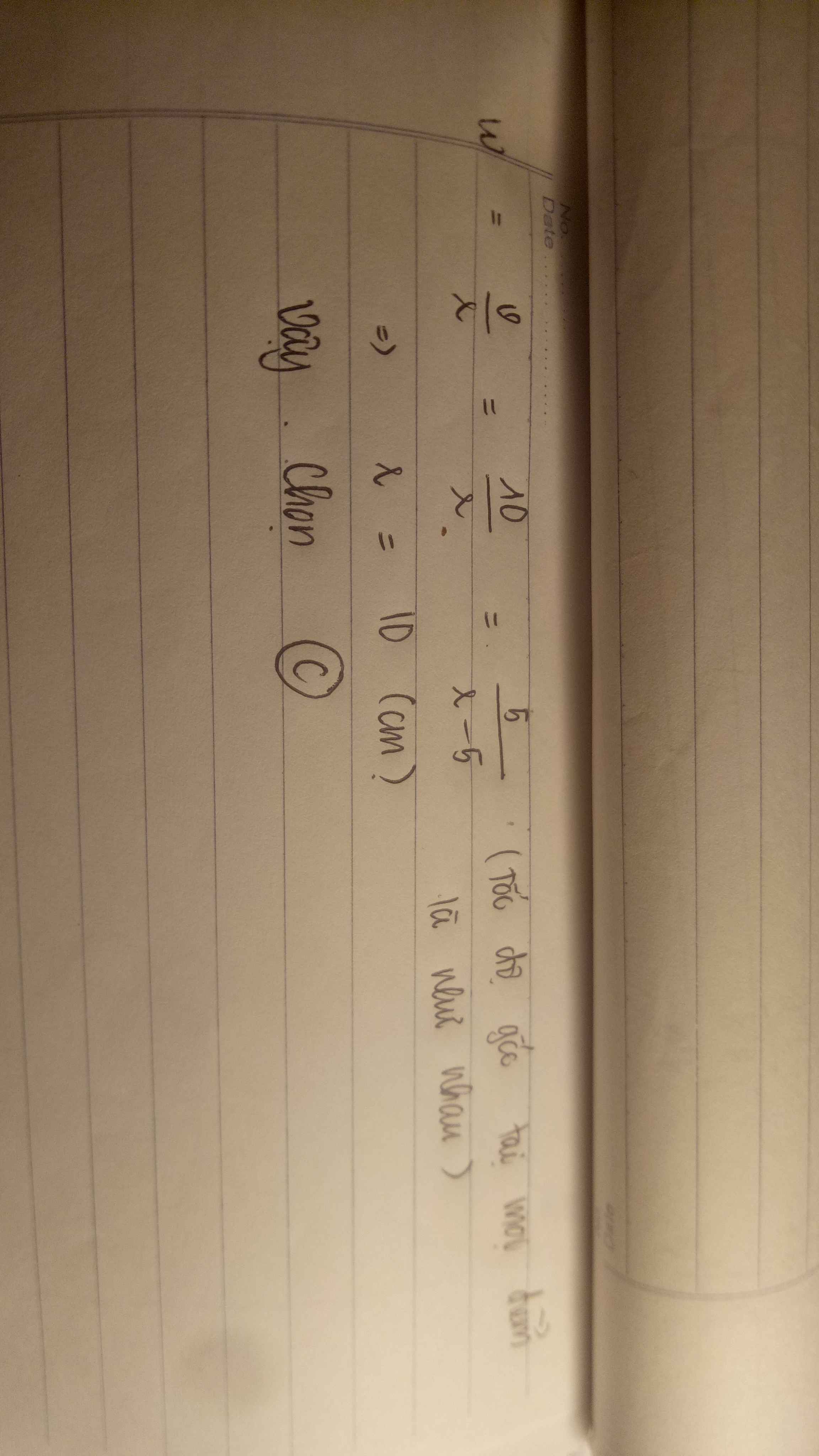



 vậy bài em làm như này sai òi hả🥲 cảm mơn
vậy bài em làm như này sai òi hả🥲 cảm mơn