Xét 8 số thực \(a_0;a_1;a_2;...;a_7\)chỉ nhận một trong ba giá trị -1;0;1. Hỏi biểu thức \(a_0+a_1.3+a_2.3^2+a_3.3^3+...+a_7.3^7\)nhận bao nhiêu giá trị không âm khác nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\left(3x^8-2x^6+x^5+2x-x^2+1\right)^5=a_0+a_1x+...+a_{40}x^{40}\)
Từ khai triển này ta thay x = 1 vào thì được
\(a_0+a_1+...+a_{40}=\left(3-2+1+2-1+1\right)^5=4^5=1024\)


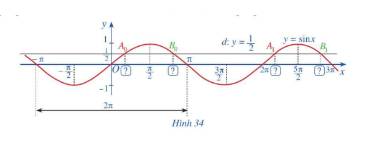
a) Hoành độ của \({A_0}\) là \(\frac{\pi }{6}\)
Hoành độ của \({B_0}\) là \(\frac{{5\pi }}{6}\)
b) Hoành độ của \({A_1}\) là \(\frac{{13\pi }}{6}\)
Hoành độ của \({B_1}\) là \(\frac{{17\pi }}{6}\)

Xét \(x\ne1\)
\(\left(1+x+...+x^{10}\right)^{11}=a_0+a_1x+...+a_{110}x^{110}\)
\(\Leftrightarrow\left(x-1\right)^{11}\left(1+x+...+x^{10}\right)^{11}=\left(x-1\right)^{11}\left(a_1+a_1x+...+a_{110}x^{110}\right)\)
\(\Leftrightarrow\left(x^{11}-1\right)^{11}=\left(x-1\right)^{11}\left(a_0+a_1x+...+a_{110}x^{110}\right)\)
\(VP=\left(x-1\right)^{11}\left(a_0+a_1x+...\right)=\left(\sum\limits^{11}_{k=0}C_{11}^kx^k\left(-1\right)^{11-k}\right)\left(a_0+a_1x+...\right)\) (1)
Ta thấy tổng các hệ số của \(x^{11}\) trong khai triển (1) là:
\(C_{11}^0\left(-1\right)^{11}.a_{11}+C_{11}^1\left(-1\right)^{10}a_{10}+C_{11}^2\left(-1\right)^9a_9+...+C_{11}^{11}\left(-1\right)^0a_0\)
\(=-C_{11}^0a_{11}+C_{11}^1a_{10}-C_{11}^2a_9+...+C_{11}^{11}a_0=-T\)
\(VT=\sum\limits^{11}_{k=0}C_{11}^k\left(x^{11}\right)^k.\left(-1\right)^{11-k}\)
Hệ số của \(x^{11}\) trong khai triển trên là \(C_{11}^1\left(-1\right)^{10}=C_{11}^1=11\)
Mà \(VT=VP\Rightarrow-T=11\Rightarrow T=-11\)

\(P=\dfrac{x^2+1}{8}+\dfrac{1}{\sqrt{x^2+1}}+\dfrac{1}{\sqrt{x^2+1}}\ge3\sqrt[3]{\dfrac{x^2+1}{8\left(x^2+1\right)}}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=\pm\sqrt{3}\)