Cho 4 điểm A, B, C, D phân biệt. Tìm vị trí điểm M sao cho: \(\overrightarrow{AM}=\overrightarrow{BC}-\overrightarrow{AD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2023
Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Cách 1:
\(\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - 4\overrightarrow {MB} \Rightarrow \frac{{MA}}{{MB}} = \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = \frac{{\left| { - 4\overrightarrow {MB} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = 4\) và hai vectơ \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng
Suy ra M nằm giữa AB sao cho \(\frac{{MA}}{{MB}} = 4\)
Cách 2:
\(\begin{array}{l}
\overrightarrow {MA} + 4\overrightarrow {MB} = \vec 0\\
\Leftrightarrow \overrightarrow {MB} + \overrightarrow {BA} + 4\overrightarrow {MB} = \vec 0\\
\Leftrightarrow 5\overrightarrow {MB} = \overrightarrow {AB}
\end{array}\)
Vậy A, M, B thẳng hàng, M nằm giữa A và B sao cho \(MB = \frac{1}{5}AB\)
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
** M là trung điểm của AB đúng không bạn?
a.
\(|\overrightarrow{AM}+\overrightarrow{AB}|=|\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}|=\frac{3}{2}|\overrightarrow{AB}|=\frac{3}{2}.3a=\frac{9a}{2}\)
b.
\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{AB}+\overrightarrow{BA}|=|\overrightarrow{0}|=0\)
c.Trên $CD$ lấy $K$ sao cho $CK=a$. Khi đó:
\(|\overrightarrow{DN}+\overrightarrow{BN}|=|\overrightarrow{DN}+\overrightarrow{KD}|=|\overrightarrow{KN}|=KN=\sqrt{a^2+a^2}=\sqrt{2}a\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) \(\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0 \)
\(\begin{array}{l}
\overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\
\Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\
\Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\
\Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB}
\end{array}\)
Vậy O thuộc đoạn AB sao cho \(OB = \frac{1}{4}AB\)
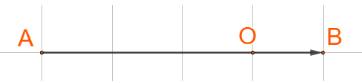
b) Ta có:
\(\begin{array}{l}
\overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\
= \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\
= 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm)
\end{array}\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
Gọi D là chân đường phân giác của góc A trên BC
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AC}{AC}=\dfrac{4}{5}\Rightarrow5\overrightarrow{BD}=4\overrightarrow{DC}\)
\(\Rightarrow5\overrightarrow{BD}=4\overrightarrow{DB}+4\overrightarrow{BC}\Rightarrow\overrightarrow{BD}=\dfrac{4}{9}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\dfrac{4}{9}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\dfrac{5}{9}\overrightarrow{AB}+\dfrac{4}{9}\overrightarrow{AC}\)
\(\Rightarrow M\) trùng D hay M là chân đường phân giác của góc A trên BC
Lấy điểm F sao cho \(\overrightarrow{AF}=\overrightarrow{BC}\) (hay dựng hbh \(ABCF\))
Trên tia đối tia AD lấy E sao cho AD=AE hay \(\overrightarrow{AD}=-\overrightarrow{AE}\)
Cộng 2 vecto \(\overrightarrow{AF}\) và \(\overrightarrow{AE}\) theo quy tắc hbh sẽ tìm được điểm M
\(\Rightarrow\overrightarrow{BC}-\overrightarrow{AD}=\overrightarrow{AF}+\overrightarrow{AE}=\overrightarrow{AM}\)