Tính cac góc tạo bơi cạnh và đường chéo của 1 hinh chữ nhật có 2 cạnhh là 3 va \(\sqrt{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Xét tam giác vuông $ABC$ có:
$\frac{AC}{BC}=\sin \widehat{ABC}$
$\Leftrightarrow \frac{AC}{12}=\sin 60^0$
$\Rightarrow AC=12.\sin 60^0=6\sqrt{3}$ (m)

B.Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi

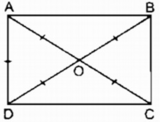
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có: AC = BD ( tính chất hình chữ nhật) ⇒ OA = OD = 1/2 AC
Lại có: AD = 1/2 AC (gt)
Suy ra: OA = OD = AD
⇒ ∆ OAD đều ⇒ ∠ (AOD ) = 60 0


Gọi O là giao điểm của hai đường chéo AC và BD.
AC = BD (tính chất hình chữ nhật)
\(\Rightarrow OA=OD=\dfrac{1}{2}AC\)
\(AD=\dfrac{1}{2}AC\left(gt\right)\)
\(\Rightarrow OA=OD=AD\)
\(\Rightarrow\Delta OAD\) đều
\(\Rightarrow\widehat{AOD}=60^0\)