Cho tam giác ABC, P là giao điểm của 3 đường phân giác trong. Từ P kẻ đương thẳng vuông góc vs PC cắt tia CA tại M và tia CB tại N. CMR a M thuộc cạnh CA và N thuộc cạnh CB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2015
bạn tự vẽ hình nhé
a. Xét tam giác CDA và tam giác CDE có CA = CE, gócACD = gócECD, CD[cạnh chung ]
=> tam giác CDA =tam giác CDE[c.g.c] => GÓC CAD = GÓC CDE = 90độ
=> DE vuông góc vs BC
b. Theo câu a, tam giác CDA = tam giác CDE
=> AD = ED
Xét tam giác ADM và tam giác EDB có :
GÓC MDA = GÓC EDB [=90ĐỘ]
AD=ED
MDA=BDE[ĐỐI ĐỈNH]
=> tam giác ADM = tam giác EDB [g-c-g]=> MA=BE=> CM=CB
DT : tam giác MEC = tam giác BAC[ch-gn]
=> EM = AB
c.Theo câu a , tam giác CDA =tam giác CDE
=>AD = AE => tam giác ADE cân tại D
=> GÓC DEA =90độ - GÓCADE / 2 [1]
Theo câu b . tg ADM = tgEDB
=> DM=DB=> tg BDM cân tại D => GÓC DMB = 90độ - góc MDB / 2 [2]
GÓC MDB= GÓC ADE [3]
Từ [1] , [2], [3]
=> GÓC AED=GÓC DMB
=> AE//MB
11 tháng 7 2017
mình vẽ hình rồi, còn phần chứng minh làm như bạn Trần Hoàng Việt nha!!
11 tháng 7 2017
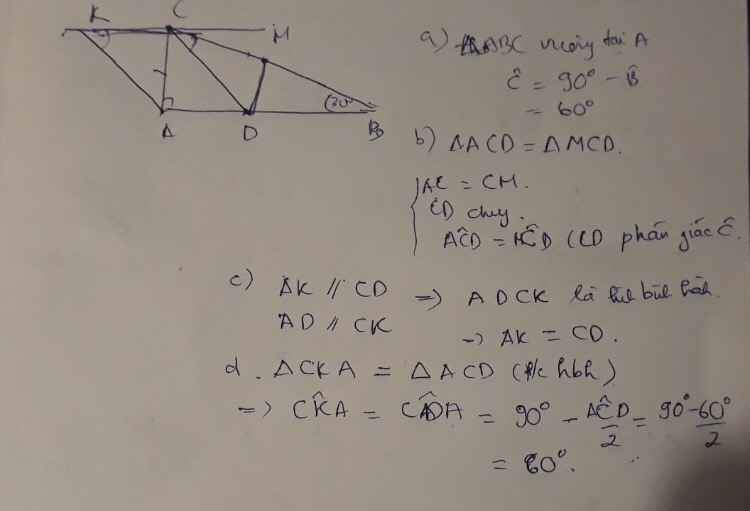
a) Ta có : A=900 ; B=300
=> C=180-A-B=180-90-30=60
b) Xét tam giác ACD và MCD ta có :
CD chung (1)
CM=CA (gt)(2)
góc ACD=góc DCM (gt) (3)
Từ (1)(2)(3) =>\(\Delta\)ACD=\(\Delta\)MCD (c.g.c)
c) Ta có :AK//CD; CK//AD => tứ giác ADCK là hình bình hành
=>AK=CD (cặp cạnh tương ứng )
d)Ta có : \(\widehat{BDC}\)=180-30-60:2=1200
\(\widehat{CPA}\)=180-120=60
Do ADCK là hình bình hành nên \(\widehat{CPA}\)=\(\widehat{AKC}\)=\(60^0\)