Cho tam giác ABC M N P lần lượt là trung điểm của BC CA AB và điểm M bất kì chứng minh vectơ AB + vectơ BC + vectơ CP = vectơ 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 11 2021
Do M là trung điểm BC nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
Tương tự: \(\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}\) ; \(\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
Cộng vế:
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BA}\right)+\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CB}\right)=\overrightarrow{0}\)
b. Từ câu a ta có:
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OM}+\overrightarrow{BO}+\overrightarrow{ON}+\overrightarrow{CO}+\overrightarrow{OP}=\overrightarrow{0}\)
\(\Leftrightarrow-\overrightarrow{OA}+\overrightarrow{OM}-\overrightarrow{OB}+\overrightarrow{ON}-\overrightarrow{OC}+\overrightarrow{OP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}\) (đpcm)
15
1
27 tháng 9 2021
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)\)
=0
nên 
CM
22 tháng 12 2017
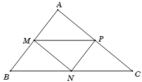
Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB.
Đáp án B
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
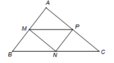
Từ giả thiết ta có PN là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{PN}=\dfrac{1}{2}\overrightarrow{BC}=\overrightarrow{BM}\)
Do đó:
\(\overrightarrow{BM}+\overrightarrow{NC}=\overrightarrow{PN}+\overrightarrow{NC}=\overrightarrow{PC}\)
b.
Theo tính chất trọng tâm: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\left(\overrightarrow{AG}+\overrightarrow{GM}\right)\)
\(\Rightarrow\dfrac{1}{3}\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{GM}\Rightarrow2\overrightarrow{MG}=-\overrightarrow{AG}=\overrightarrow{GA}\)
\(\Rightarrow\overrightarrow{GB}+\overrightarrow{GC}+2\overrightarrow{MG}=\overrightarrow{GC}+\overrightarrow{GB}+\overrightarrow{GA}=\overrightarrow{0}\)
AH
Akai Haruma
Giáo viên
22 tháng 10 2020
Lời giải:
a)
$2\overrightarrow{AD}=\overrightarrow{AD}+\overrightarrow{AD}$
$=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{CD}$
$=\overrightarrow{AB}+\overrightarrow{AC}+(\overrightarrow{BD}+\overrightarrow{CD})$
$=\overrightarrow{AB}+\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AD}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$
Tương tự:
$\overrightarrow{BE}=\frac{\overrightarrow{BC}+\overrightarrow{BA}}{2}$
$\overrightarrow{CF}=\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}$
Cộng lại:
$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\frac{\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\frac{\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}}{2}=\overrightarrow{0$}$
Ta có đpcm.
b)
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MD}+\overrightarrow{DA}+\overrightarrow{ME}+\overrightarrow{EB}+\overrightarrow{MF}+\overrightarrow{FC}$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})+(\overrightarrow{DA}+\overrightarrow{EB}+\overrightarrow{FC})$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})-(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF})$
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}-\overrightarrow{0}$ (theo phần a)
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}$
Ta có đpcm.
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 10 2020
1.
\(\left\{{}\begin{matrix}\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BN}\\\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CP}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\overrightarrow{AB}+\overrightarrow{BC}=2\overrightarrow{BN}\\\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{CB}=2\overrightarrow{CP}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AB}-\overrightarrow{BC}=-2\overrightarrow{BN}\\\overrightarrow{AB}+2\overrightarrow{BC}=-2\overrightarrow{CP}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\overrightarrow{AB}-2\overrightarrow{BC}=-4\overrightarrow{BN}\\\overrightarrow{AB}+2\overrightarrow{BC}=-2\overrightarrow{CP}\end{matrix}\right.\)
\(\Rightarrow3\overrightarrow{AB}=-4\overrightarrow{BN}-2\overrightarrow{CP}\Rightarrow\overrightarrow{AB}=-\frac{4}{3}\overrightarrow{BN}-\frac{2}{3}\overrightarrow{CP}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 10 2020
2.
\(\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DI}\)
\(=-\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC}\)
\(=-\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{BI}=-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=\overrightarrow{AB}+\frac{1}{3}\left(\overrightarrow{BI}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AB}+\frac{1}{3}\left(-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}=\frac{5}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}\)
Dạ hik như đề sai ạ \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CP}=\overrightarrow{AP}\)
mà P là trung điểm của AB nên \(\overrightarrow{AP}\ne0\)