Cho góc nhọn xOy , trên tia Ox lấy điểm A , trên tia Oy lấy điểm B . Từ A kẻ đường thẳng vuông góc với Ox , cắt Oy tại C . Từ B kẻ đường thẳng vuông góc với Oy , cắt Ox tại D .CMR: AC=BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KP
19 tháng 4 2022
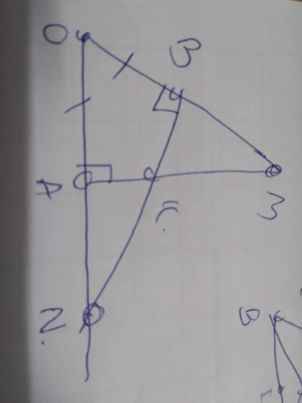
hình bạn tự vẽ nha
có: MA⊥Ox(gt)=>△OAM vuông tại A
MB⊥Oy(gt)=>△OBM vuông tại B
xét △ vuông OAM và △vuông OBM có:
OA=OB(gt)
OM chung
=> △ vuông OAM = △vuông OBM ( cạnh huyền cạnh góc vuông )
=> AM=BM( 2 cạnh tương ứng )
=> M thuộc đường trung trực của AB
mà OA=OB(gt)=> O thuộc đường trung trực của AB
=> OM là đường trung trực của AB hay OM⊥AB
trong △ OAB có:
AC⊥OB=> AC là đường cao thứ nhất của △ OAB
BD⊥OA=> BD là đường cao thứ hai của △ OAB
OM⊥AB=> OM là đường cao thứ ba của △ OAB
=> AC,BD, OM đồng quy tại 1 điểm
16 tháng 1 2021
a, NỐi O với I
Xét Tam giác OAI và tam giác OBI có
OA=OB
A=B=90 độ
OI chung
=>HAI tam giác bằng nhau
=>AI=BI (t/ư)
=>tam giác AIB cân tại I
5 tháng 12 2023
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOB}\) chung
Do đó: ΔOAM=ΔOBN
=>\(\widehat{OMA}=\widehat{ONB}\) và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
\(\widehat{KNA}=\widehat{KMB}\)
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>\(\widehat{AOK}=\widehat{BOK}\)
=>OK là phân giác của \(\widehat{AOB}\)
5 tháng 12 2023
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
chung
Do đó: ΔOAM=ΔOBN
=> và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>
=>OK là phân giác của
5 tháng 12 2023
Xin lỗi bạn, hồi nãy câu trả lời của mình bị lỗi. Giờ mình xin phép sửa lại chút nha:
23 tháng 2 2022
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOM}\) chung
Do đó: ΔOAM=ΔOBN
b: Xét ΔBMN vuông tại B và ΔANM vuông tại A có
NM chung
BN=AM
Do đó: ΔBMN=ΔANM
Suy ra: \(\widehat{IMN}=\widehat{INM}\)
hay ΔIMN cân tại I
19 tháng 12 2016
a) Xét 2 tam giác vuông OAC và tam giác OBD có:
OA = OB (gt)
O là góc chung
suy ra tam giác OAC = tam giác OBD (cạnh góc vuông - góc nhọn kề cạnh ấy)
b) Ta có : OD = OA + AD
OC = OB + BC
mà OD = OC (vì tam giác OAC = tam giác OBD)
OA = OB ( gt)
suy ra AD = BC
Xét 2 tam giác vuông ADI và tam giác BCI có:
AD = BC (cmt)
góc D = góc C (vì tam giác OAC = tam giác OBD)
suy ra tam giác ADI và tam giác BCI (cạnh goác vuông - góc nhọn kề cạnh ấy)
suy ra IA = IB (2 cạnh tương ứng)
c)Xét 2 tam giác vuông OAI và tam giác OBI có:
OI là cạnh chung
OA = OB (gt)
suy ra tam giác OAI = tam giác OBI (2 cạnh góc vuông)
suy ra góc O1 = góc O2 (2 góc tương ứng)
suy ra OI là tia phân giác của góc xOy
Cái chỗ A1, A2, B1, B2 bạn đừng kí hiệu vào bài làm nhé!
Mình nhầm tí!
25 tháng 4 2023
Gỉa sử đường trung trực của OA cắt OA tại H; đường trung trực của OB cắt OB tại K
Vì HI là đường trung trực của OA nên IO = IA (tính chất đường trung trực của đoạn thẳng)
Vì KI là đường trung trực của OB nên IO = IB (tính chất đường trung trực của đoạn thẳng)
25 tháng 4 2023
b: Xet ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
góc O chung
=>ΔOAE=ΔOBF
=>OE=OF
a: 
Không thể bằng nhau được bạn ạ mà chỉ xảy ra TH đồng dạng vì đâu có cặp cạnh nào bằng nhau cho trước sẵn đâu
\(\hept{\begin{cases}OA\ne OB\\OD\ne OC\end{cases}}\)
Mik nghĩ cần bổ sung thêm OB=OA.
Xét tam giác OAC và OBD có:OA=OB,^OBD=^OAC,^AOB chung
Khi đó \(\Delta\)OAC=\(\Delta\)OBD ( ch-gn ) => AC=BD