Cho đường tròn tâm O bán kính 3cm. Từ một điểm A cách O là 5cm vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm).
a) Chứng minh AO vuông góc với BC
b) Kẻ đường kính BD. Chứng minh rằng DC song song với OA;
c) Tính chu vi và diện tích tam giác ABC.
d) Qua O kẻ đường thẳng vuông góc với BD, đường thẳng này cắt tia DC tại E. Đường thẳng AE và OC cắt nhau ở I; đường thẳng OE và AC cắt nhau ở G.
Chứng minh IG là trung trực của đoạn thẳng OA.

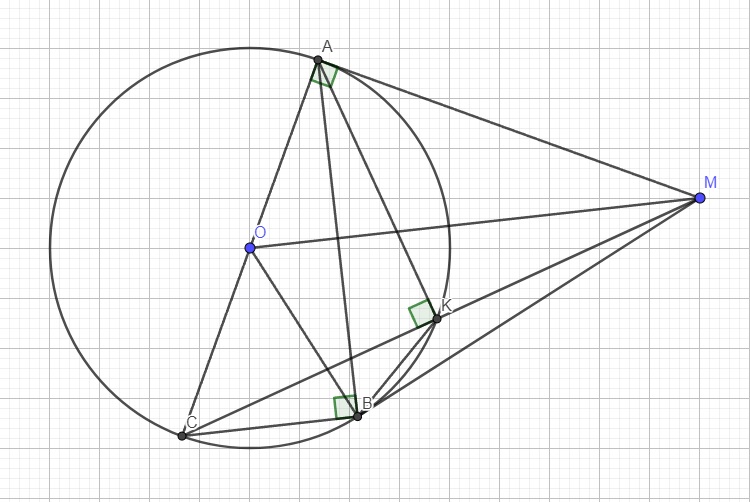
Tham khảo:
a) theo tính chất 2 tiếp tuyến cắt nhau => ab=ac -> a thuộc trung trực bc
từ ob = oc(gt) => o thuộc trung trực bc
từ 2 ý trên => ao là trung tực của bc => ao vuông góc bc
b) từ ao là trung trực của bc (cmt) => bh=hc
trong tam giác bdc có :
bh=hc(cmt)
ob=do(dt)
=> i là đường tb của tam giác bdc => oh song song dc=> dc song song oa
c)áp dụng định lí py ta go vào tam giác oba
ob^2 + ba^2 = oa^2
<=> 3^2 + ba^2 = 5^2
<=> ba =4 (cm)
áp dụng hệ thức lượng tam giác oba có
ba^2 = ha. oa
<=> 4^2 = ha. 5
<=> ha=302 (cm)
=> oh = 1.8 (cm)
áp dụng hệ thức lượng vào tam giác oba có
bh^2 = oh.ha
<=>bh= 2.4(cm)
mà bh=hc(cmt)=> bc=4.8(cm)
chu vi abc = ab+ bc+ac=12.8(cm)
ta có ha+ho=oa=> ha= 3.2(cm)
diện tích abc = 1/2 . ah.bc= 7.68(cm^2)
d) ta có oe vuông bd(gt)
ba vuông bd(gt)
=> oe song song ba => góc boa = góc oai (slt)(3)
trong tam giác obc có oh vuông bc (cmt) => oh là đcao
mà hb=hc(cmt)=> oh đồng thời là trung tuyến => tam giác obc cân tại o => oh là phân giác góc boc
=> góc oai = góc ioa
=> tam giác oai cân tại i
=> oi =ai
=> i thuộc trung trực oa(5)
trong tamgiác oae có góc eoa + góc oae = aeo (*)
trong tgiác oba có góc boa + góc bao = 90 độ (**)
mà aoe =bao(slt)(1)
oae = boa (slt) (2)
từ (*)(**)(1)(2) => aeo = 90 độ
xét tgiác ogc và tam giác age có aeg= ocg =90 độ
ogc=age(đối đỉnh)
=> hai tgiác đồng dạng (gg)
=> ioe=cai
ta có; ioe+eoa =ioa (7)
cai+oac =oai (8)
mà ioa = dai (cmt)(9)
ioe =cai(cmt) (10)
từ (7)(8)(9)(10) => eoa = oac
=> tgiác oag cân tại g
=> og=ag
=> g thuộc trung trực ao(6)
từ (5)(6) => ig là trung trực ao