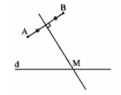
Cho đường thẳng d và hai điểm A, B nằm khác phía đối với d. Tìm M thuộc d sao cho MA + MB ngắn nhất. (Các bạn nhớ vẽ hình nha.)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2019
Cách giải
- Bước 1: Tìm điẻm A’ đối xứng với A qua đường thẳng d
- Bước 2: Nối A’B , đường thẳng này cắt d tại M . Là điểm cần tìm
- Bước 3: Chứng minh M là điểm duy nhất .
Study well
CM
17 tháng 1 2018
a) Các bộ ba điểm thẳng hàng: A, B, C; D, B, E
b) Hai điểm A và B nằm cùng phía với điểm C.
c) Hai điểm D và E nằm khác phía với B.
Hai điểm A và C nằm khác phía với B.
d) Điền các kí hiệu ∈ hay ∉ vào ô trống:
14 tháng 4 2016
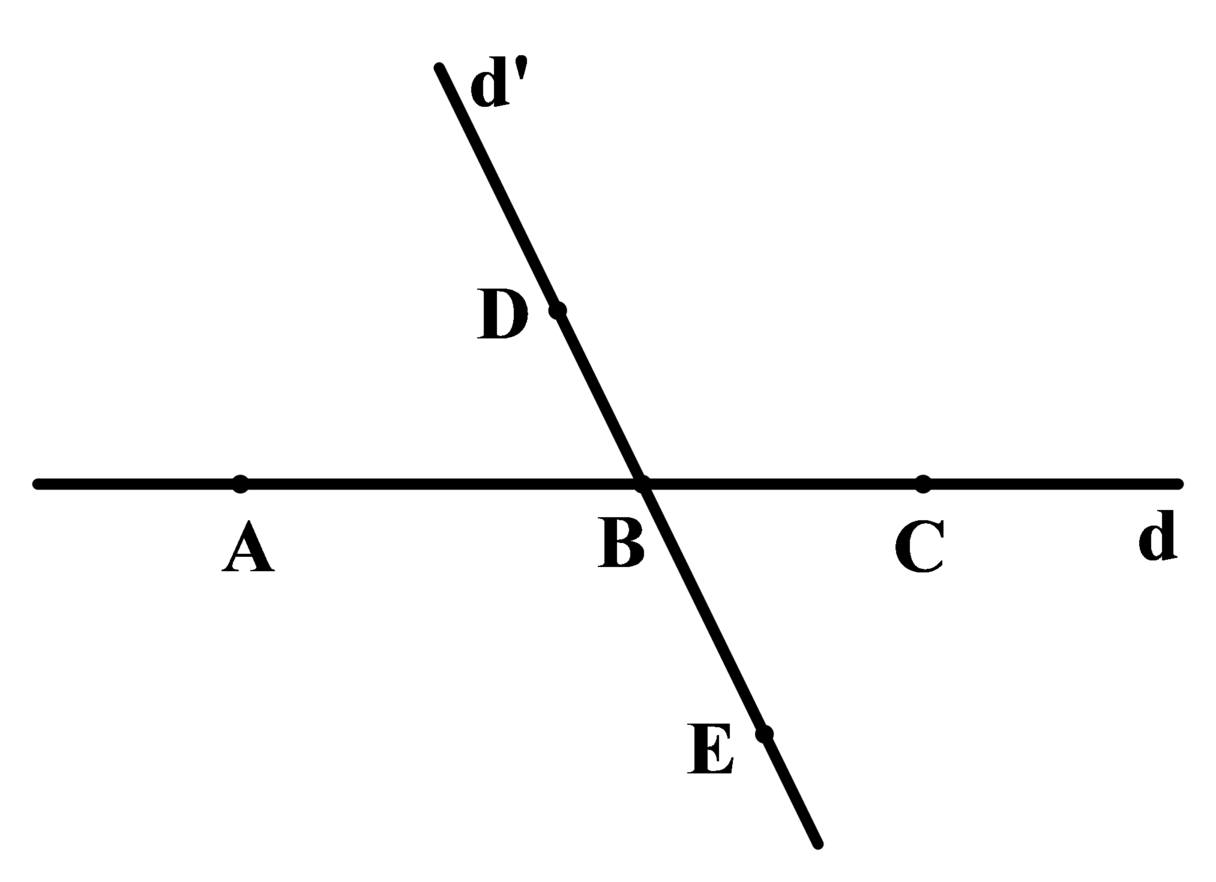
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’. Do đó : MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’
20 tháng 10 2018
Làm sao tìm được điểm đối xứng vậy bạn? Mình không hiểu rõ (trong mặt phẳng tọa độ nhà)
2 tháng 2
a: Các điểm nằm cùng phía đối với C là D,B
Các điểm nằm khác phía so với C là A,D; A,B
b: Các tia trùng nhau gốc C là CD,CB
Các tia đối nhau gốc C là CA và CB
CM
18 tháng 10 2019
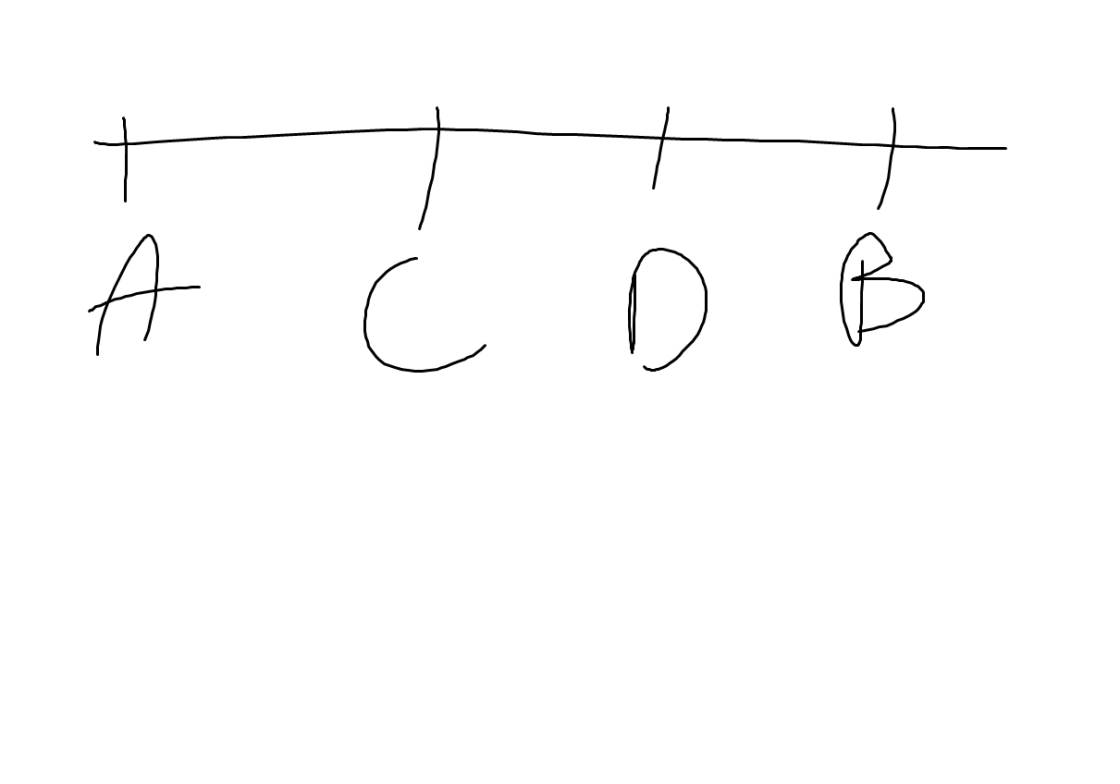
Ta có |MA − MB| ≥ 0 với một điểm M tùy ý và |MA − MB| = 0 chỉ với các điểm M mà MA = MB, tức là chỉ với các điểm M nằm trên đường trung trực của đoạn thẳng AB.
Mặt khác M phải thuộc d. Vậy M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB. Có giao điểm này vì AB không vuông góc với d.
Tóm lại: Khi M là giao điểm của d và đường trung trực của đoạn thẳng AB thì |MA − MB| đạt giá trị nhỏ nhất và bằng 0.
CM
31 tháng 7 2019
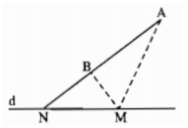
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Theo hệ quả bất đẳng thức tam giác ta có:
|MA−MB| < AB
Khi M ≡ N thì
|MA−MB|= AB
Vậy |MA−MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.