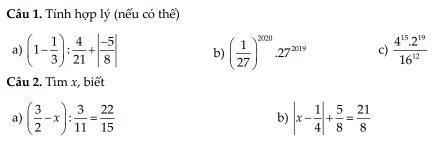
Giải giúp em 3 bài a b c câu 1 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



III.
1. appearance sau tính từ thì sẽ là danh từ
2. necessary sau động từ tobe trong trường hợp này thì cũng là tính từ luông
3. happily câu này thì mình áp dụng cấu trúc mà v+adv
4. interesting cái này thì mình nghe cô mình nói là nếu mà mình nói cái gì, hay ai đó thú vị thì mình sẽ dùng interesting, còn nếu mình nói mình hay ai đó do cái gì hay ai đó làm cho cảm thấy thú vị thì là interested.
5. pollution còn air pollution thì cơ bản là nói về ô nhiễm không khí thôi
6. preparation sau tính từ thì sẽ là danh từ
IV.
1. c on➜in, người ta có cái quy định á, là in the month, on the day, at the time
2. d celebrating➜celebrated, theo như tui hiểu thì nó như là passive voice á
3. b who➜which, mount pinatubo đâu phải là nói về ai đâu, mà người ta đang nói tới cái núi mà, với lại đằng sau nữa là kiểu giới thiệu về núi á nên là mình đổi như vậy
4. b therefore➜because, dịch nam bị ướt vì anh ấy đã quên mang dù vào ngày hôm qua
uhmmmm...tui cx hong chắc lắm đâu mà nếu bạn còn gì thắc mắc thì cứ hỏi nghen, tại mấy cái đó là tui mới nghĩ ra tạm thời thôi á

Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng

1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)

b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED



\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
\(a,=\dfrac{2}{3}\cdot\dfrac{21}{4}+\dfrac{5}{8}=\dfrac{7}{2}+\dfrac{5}{8}=\dfrac{33}{8}\\ b,=\left(\dfrac{1}{27}\cdot27\right)^{2020}\cdot27=1^{2020}\cdot27=27\\ c,=\dfrac{2^{30}\cdot2^{19}}{2^{48}}=2\)