Cho tứ giác ABCD có AB=CD, AD=BC.Chứng minh AB ssong song CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
26 tháng 11 2022
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
US
1
NH
17 tháng 9 2020
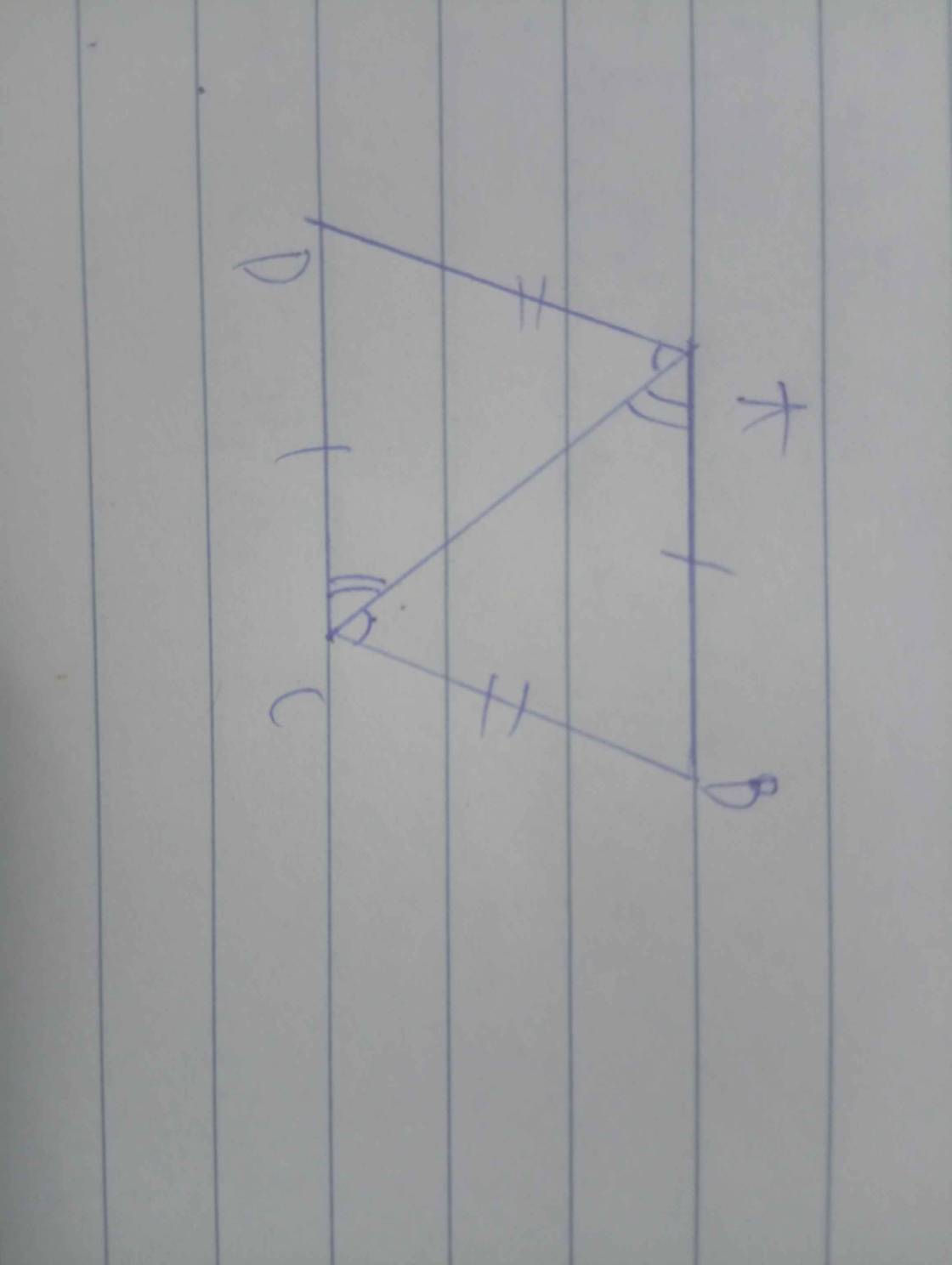
\(\text{AB song song với CD và AB=CD}\Rightarrow ABCD\text{ là hình bình hành}\)
\(\Rightarrow AD\text{//}BC\text{ và }AD=BC\)
NK
19 tháng 4 2017
Áp dụng t/c đường trung bình của tam giác vào tam giác DAB có :
E trung điểm AD ; I trung điểm BD
=> EI // AB.
Áp dụng t/c đường trung bình của tam giác vào tam giác DBC có :
F trung điểm BC ; I trung điểm BD
=> IF // DC
LN
Lưu Nguyễn Hà An
CTVHS
11 tháng 8 2023
Tham khảo nha, tuy ko trùng đề lắm
Gọi trung điểm dường cheo AC, BD lần lượt là M, N
MN cắt AB, CD lần lượt ở I, K
Ta cần chứng minh góc NIB = góc MKC
Lấy H là trung điểm BC. Nối MH, NH.
Xét tam giac ABC có AM = MC ; CH = HB => MH là đường trung bình tam giác ABC => MH =AB/2 (1) và MH // AB => góc KMH = góc INH (2)
chung minh tuong tu ta có: NH = CD/2 (3)và NH // CD =>góc INH = góc MKC (4)
Mat khac từ (1)và (3) ta có NH = MH vì đều bằng một nửa AB và CD => tam giác MHN cân tại H => góc NMH = góc MNH =>góc KMH = góc INH (vì kể với 2 góc bằng nhau) (5)
Từ (3)(4)(5) => góc MKC = góc NIB (đpcm)
8 tháng 7 2018
Vì \(\hept{\begin{cases}EA=ED\\FB=FC\end{cases}}\)(GT)
=> EF lầ đường trung bình
=> AB // CD
=> ABCD là hình thang
Vì có EF là đường trung bình
=> \(EF< \frac{AB+DC}{2}\)( đpcm )
( Tính chất đường trung bình của hình thang )
7 tháng 5 2019
+) Chứng minh nếu AD // BC thì đường tròn (I) đường kính CD tiếp xúc AB:
Gọi tiếp điểm giữa (O) và CD là H .Từ I hạ IK vuông góc AB tại K.
Khi đó tứ giác KOHI nội tiếp đường tròn (OI) => ^KHI = ^KHD = ^KOI
Dễ thấy tứ giác ABCD là hình thang (Vì BC // AD) có đường trung bình OI nên OI // BC // AD
=> ^KOI = ^KBC. Do đó ^KHD = ^KBC => Tứ giác BKHC nội tiếp. Tương tự, tứ giác ADHK nội tiếp
Từ đó ^DKC = ^DKH + ^CKH = ^DAH + ^CBH. Kết hợp với AD // BC suy ra ^DKC = ^BHA = 900
=> Điểm K thuộc đường tròn (I). Mà AB vuông góc IK tại K nên (I) tiếp xúc AB (*)
+) Chứng minh nếu (I) đường kính CD tiếp xúc với AB thì AD // BC:
Ta gọi tiếp điểm giữa (I) và AB là K, qua K kẻ đường thẳng song song với AH cắt CD tại C'
Lúc này, ^KC'I = ^AHD = ^ABH. Ta có KC' // AH; AH vuông góc BH => KC' vuông góc BH
Do KI vuông góc AB nên ^IKC' = ^ABH. Suy ra ^KC'I = ^IKC' => \(\Delta\)KIC' cân tại I
=> IC' = IK = IC. Mà C và C' nằm cùng phía so với IK nên C trùng C'.
Từ đây ^KCH = ^AHI = ^KBH => Tứ giác KHCB nội tiếp. Hoàn toàn tương tự, tứ giác AKHD nội tiếp
Vậy thì ^HCB = ^HKA = 1800 - ^ADH => AD // BC (**)
+) Qua (*) và (**), ta thu được ĐPCM.