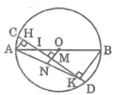
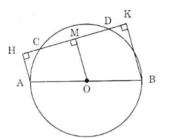
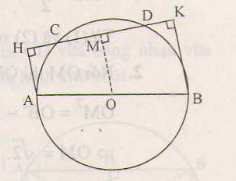
Cho đường tròn (O) đường kính AB=2R ,dây CD cắt đường kính AB. Gọi M,N theo thứ tự là chân các đường vuông góc hạ từ A,B đến đường thẳng CD
a. Chứng minh rằng các điểm M,N nằm ngoài đường tròn
b. Tính diện tích lớn nhất của tứ giác AMNB theo R biết CD=R
Các bạn làm ơn giupos mình với !!! Cảm ơn nhiều !!!