Cho tam giac ABC vuông tại A co AB=3cm,AC=4cm,BC=5cm. Kẻ BM là tia phân giác của góc ABC,MH vuông góc với BC.
a) Chứng minh tam giác MBA=tam giác BMH
b)Chứng minh AM<MC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
P
22 tháng 4 2017
nhớ tk cho ming nha
1, Xét tam giác ABC có :
\(BC^2=AC^2+AB^2\)
\(\Leftrightarrow BC^2=4^2+3^2\)
\(\Leftrightarrow BC^2=25\)
\(\Leftrightarrow BC=5\left(cm\right)\)
2,Ta có :\(\widehat{BMA}+\widehat{MBA}=90^O\)
\(\widehat{BMH}+\widehat{MBH}=90^O\)
MÀ \(\widehat{ABM}=\widehat{HBM}\)
Nên \(\widehat{BMA}=\widehat{BMH}\)
Xét tam giác ABM và tam giác HBM có :
\(\widehat{ABM}=\widehat{HBM}\left(gt\right)\)
\(BMchung\)
\(\widehat{BMA}=\widehat{BMH}\)
\(\Rightarrow\Delta BAM=\Delta BHM\left(c.g.c\right)\)
3,Vì \(\Delta BAM=\Delta BHM\Rightarrow AM=MH\left(1\right)\)
Xét \(\Delta HMC\)có :
\(\widehat{MHC}=90^0\)
Suy ra :MC>MH(2)
Từ (1) và(2):AM<MC
4,Ta có :\(\widehat{AMH}+\widehat{HMC}=180^0\left(1\right)\)
Xét tam giác NMA và tam giác CMH có:
\(HC=NA\)
\(\widehat{NAM}=\widehat{CHM}\)
\(MA=MH\left(\Delta BAM=\Delta BHM\right)\)
\(\Rightarrow\Delta NMA=\Delta CMH\left(c.g.c\right)\)
\(\Rightarrow\widehat{NMA}=\widehat{CMH}\)(2)
Từ (1) và(2) : => N,M,H thẳng hàng
H
10 tháng 5 2022
a. Xét △ABD vuông tại A và △EBD vuông tại E:
\(\widehat{ABD}=\widehat{ABE}\) (BD là tia phân giác \(\widehat{ABC}\))
BD chung
=> △ABC= △EBD (ch-gn)
b.
△ ABC= △ EBD => BA=BE; AD=DE
=> B ∈ đường trung trực của AE (1)
=> D ∈ đường trung trực của AE (2)
Từ (1) và (2) => BD là đường trung trực của AE
c.
Áp dụng định lý Py-ta-go vào △ BED có:
BD2=BE2 + DE2
BD2 = 42 + 32 = 16 + 9
BD2 = 25
=> BD = 5 cm
d.
Xét △EDC có: DC > DE (cạnh huyền > cạnh góc vuông)
Mà DE=AD nên AD < DC
KV
11 tháng 3 2023
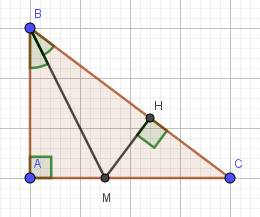
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
14 tháng 5 2022
a: BC=5cm
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
c: \(\widehat{MAH}+\widehat{BHA}=90^0\)
\(\widehat{CAH}+\widehat{BAH}=90^0\)
mà \(\widehat{BHA}=\widehat{BAH}\)
nên \(\widehat{MAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc MAC
7 tháng 4 2020
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
LA
8 tháng 4 2020
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
6 tháng 3 2022
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAE có
BH là đường cao
BH là đường trung tuyến
DO đó:ΔBAE cân tại B
hay BA=BE
c: Xét ΔCAE có
CH là đường cao
CH là đường trung tuyến
Do đó:ΔCAE cân tại C
mà CB là đường cao
nên CB là tia phân giác của góc ACE
d: Xét ΔCAB và ΔCEB có
CA=CB
BA=BE
BC chung
DO đó:ΔCAB=ΔCEB
Suy ra: \(\widehat{CAB}=\widehat{CEB}=90^0\)
hay ΔBEC vuông tại E