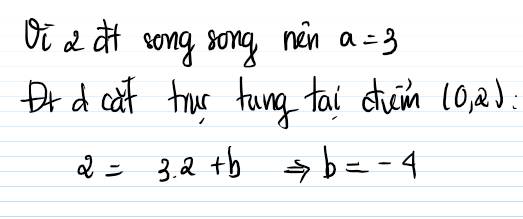xác định các hệ số a và b để đường thẳng y=ax+b cắt trục tung tại điểm có tung độ bằng -2 và song song với đường thẳng OA, trong đó O là gốc tọa độ, \(A\left(\sqrt{2};1\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
26 tháng 7 2017
Lời giải:
Vì đường thẳng $OA$ đi qua gốc tọa độ nên gọi PTĐT $OA$ là \(y=cx\)
Vì \(A(\sqrt{2},1)\) nên \(1=\sqrt{2}c\Rightarrow c=\frac{1}{\sqrt{2}}\)
Do đó PTĐT \(OA\) là \(y=\frac{x}{\sqrt{2}}\)
Đường thẳng \(y=ax+b\) song song với $OA$ nên \(a=c=\frac{1}{\sqrt{2}}\)
Mà đường thẳng trên cắt trục tung tại tung độ \(-2\) nên:
\(-2=\frac{1}{\sqrt{2}}.0+b\rightarrow b=-2\)
Vậy \((a,b)=\left (\frac{1}{\sqrt{2}},-2\right)\)
G
5 tháng 11 2019
Lời giải:
Vì đường thẳng $OA$ đi qua gốc tọa độ nên gọi PTĐT $OA$ là \(y=cx\)
Vì \(A(\sqrt{2},1)\) nên \(1=\sqrt{2}c\Rightarrow c=\frac{1}{\sqrt{2}}\)
Do đó PTĐT \(OA\) là \(y=\frac{x}{\sqrt{2}}\)
Đường thẳng \(y=ax+b\) song song với $OA$ nên \(a=c=\frac{1}{\sqrt{2}}\)
Mà đường thẳng trên cắt trục tung tại tung độ \(-2\) nên:
\(-2=\frac{1}{\sqrt{2}}.0+b\rightarrow b=-2\)
Vậy \((a,b)=\left (\frac{1}{\sqrt{2}},-2\right)\)
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Đề không rõ ràng. Bạn coi lại đề. Những dữ kiện trên được chia theo phần hay là cả 1 cụm?
H
26 tháng 2 2023
Ta có \(\left(d\right):y=ax+b\) song song với \(\left(d\right):y=3x-1\)
\(\Rightarrow a=3\) ta được phương trình \(y=3x+b\)
đường thẳng này cắt trục tung tại tung độ bằng 2
\(\Rightarrow\left(0;2\right)\)
\(\Rightarrow2=3.0+b\\ \Rightarrow b=2\)
KT
6 tháng 1 2019
a) Đồ thị hàm số đi qua gốc tọa độ
=> có dạng y = ax
=> b = 0
Đồ thị hàm số có hệ số góc bằng -2
=> y = -2x
27 tháng 7 2021
a) Thay x=0 và y=0 vào (d), ta được:
\(\left(2m-1\right)\cdot0+m=0\)
\(\Leftrightarrow m=0\)
b) Thay x=0 và y=2 vào (d), ta được:
\(\left(2m-1\right)\cdot0+m=2\)
\(\Leftrightarrow m=2\)
c) Để (d)//y=x-5 thì \(\left\{{}\begin{matrix}2m-1=1\\m\ne-5\end{matrix}\right.\Leftrightarrow m=1\)