Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a AD=AA'=2a Khoảng cách giữa hai đường thẳng AC và DC' bằng
MIng mọi người giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
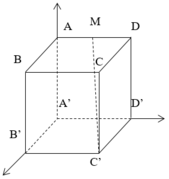
Chọn hệ trục tọa độ như hình vẽ
A'(0;0;0), B'(4a;0;0), C'(4a;4a;0), M'(0;2a;2a)
A ' B ' → 4 a ; 0 ; 0 , C ' M → - 4 a ; - 2 a ; 2 a ⇒ A ' B ' → , C ' M → = 0 ; - 8 a 2 ; - 8 a 2 A ' M → 0 ; 2 a ; 2 a d ( A ' B ' , C ' M ) = A ' B ' → , C ' M → A ' M A ' B ' → , C ' M → = 32 a 3 8 2 a 2 = 2 2 a

Đáp án A
Chọn hệ trục tọa độ như hình vẽ
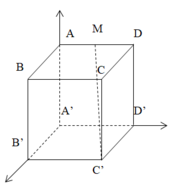
A ' ( 0 ; 0 ; 0 ) , B ' ( 4 a ; 0 ; 0 ) , C ' ( 4 a ; 4 a ; 0 ) , M ( 0 ; 2 a ; 2 a ) A ' B ' → ( 4 a ; 0 ; 0 ) , C ' M → ( − 4 a ; − 2 a ; 2 a ) ⇒ [ A ' B ' → , C ' M → ] = ( 0 ; − 8 a 2 ; − 8 a 2 ) A ' M → ( 0 ; 2 a ; 2 a ) d ( A ' B ' , C ' M ) = [ A ' B ' → , C ' M → ] A ' M → [ A ' B ' → , C ' M → ] = 32 a 3 8 2 a 2 = 2 2 a

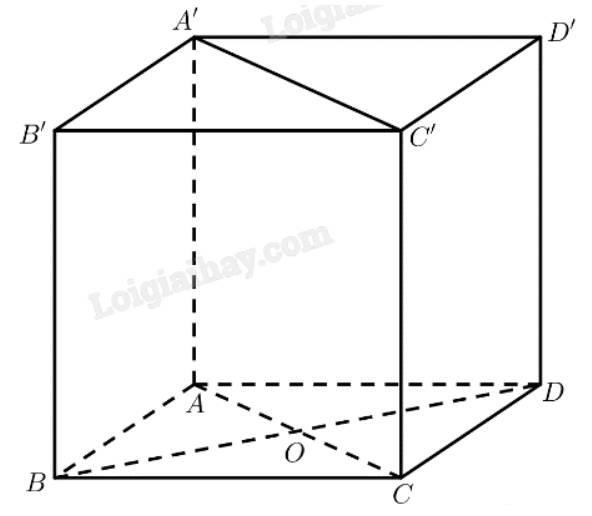
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)