Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Sửa đề: Chứng minh bốn điểm A,D,H,E cùng nằm trên đường tròn
Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
=>ADHE là tứ giác nội tiếp đường tròn đường kính AH
=>Tâm O là trung điểm của AH
b: Gọi giao điểm của AH với BC là M
Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại M
OD=OH
=>ΔODH cân tại O
=>\(\widehat{ODH}=\widehat{OHD}\)
mà \(\widehat{OHD}=\widehat{BHM}\)(hai góc đối đỉnh)
và \(\widehat{BHM}=\widehat{BCD}\left(=90^0-\widehat{DBC}\right)\)
nên \(\widehat{ODH}=\widehat{DCB}\)
ΔDBC vuông tại D có DI là đường trung tuyến
nên DI=IB=IC=BC/2
IB=ID
=>ΔIDB cân tại I
=>\(\widehat{IBD}=\widehat{IDB}\)
\(\widehat{ODI}=\widehat{ODB}+\widehat{IDB}\)
\(=\widehat{IBD}+\widehat{DCB}=90^0\)
=>DI là tiếp tuyến của (O)

Ta có H là trực tâm tg ABC
\(\Rightarrow\widehat{EAH}=\widehat{ECB}\left(cùng.phụ.\widehat{ABC}\right)\left(1\right)\)
Mà \(OA=OE\Rightarrow\widehat{AEO}=\widehat{EAO}\left(2\right)\)
Vì EM là tt ứng cạnh huyền BC của tg EBC nên \(EM=MC\)
\(\Rightarrow\widehat{ECM}=\widehat{CEM}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{AEO}=\widehat{CEM}\)
Mà \(\widehat{AEO}+\widehat{OEC}=\widehat{AEC}=90^0\Rightarrow\widehat{OEC}+\widehat{CEM}=90^0=\widehat{OEM}\)
Do đó \(OE\perp EM\) hay EM là tt của (O)

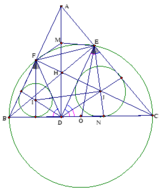
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
Tứ giác BFEC có B E C ^ = B F C ^ = 90 0
=> tứ giác BFEC nội tiếp đường tròn đường kính BC
Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF
∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^
∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)
=> ME=AH:2= MH do đó ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^
Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)
Nên O E B ^ + M E H ^ = 90 0 Suy ra M E O ^ = 90 0
⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^ = DFC ^
Tứ giác AFDC có A F C ^ = A D C ^ = 90 0 nên tứ giác AFDC nội tiếp đường tròn => B D F ^ = B A C ^
∆ BDF và ∆ BAC có B D F ^ = B A C ^ (cmt); B ^ chung do đó ∆ BDF ~ ∆ BAC(g-g)
Chứng minh tương tự ta có ∆ DEC ~ ∆ ABC(g-g)
Do đó ∆ DBF ~ ∆ DEC ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)
Vì ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác ⇒ D I D F = D J D C (2)
Từ (1) và (2) suy ra ∆ DIJ ~ ∆ DFC (c-g-c) => DIJ ^ = DFC ^

Gọi O là trung điểm của BC
góc AFH+góc AEH=180 độ
=>AFHE nội tiếp đường tròn đường kính AH
=>AFHE nội tiếp (M)
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>BFEC nội tiếp (O)
góc MFO=góc MFH+góc OFH
=góc MHF+góc OCF
=góc FBC+góc FCB=90 độ
=>MF là tiếp tuyến của (O)
Xét ΔMFO và ΔMEO có
MF=ME
OF=OE
MO chung
=>ΔMFO=ΔMEO
=>góc MEO=90 độ
=>ME là tiếp tuyến của (O)
Bạn cần phải chứng minh E, F ϵ ( O ) nữa nhé, vì vẫn có thể xảy ra trường hợp ME, MF là cát tuyến hoặc nằm ngoài ( O ). Phần này thì dùng đường trung tuyến trong tam giác vuông là xong.

Giải thích các bước giải:
a. Gọi OO là trung điểm AHAH
Xét tam giác AEHAEH vuông tại HH: OO là trung điểm AH⇒AO=OH=OEAH⇒AO=OH=OE
Chứng minh tương tự ⇒AO=OH=OD⇒AO=OH=OD
⇒OA=OH=OD=OE⇒OA=OH=OD=OE
Vậy A,D,H,E∈(O)A,D,H,E∈(O) với OO là trung điểm AHAH
b. Có: BD∪CE=H⇒HBD∪CE=H⇒H là trực tâm tam giác ABCABC
⇒AH⊥BC⇒AH⊥BC
Mà: CE⊥ABCE⊥AB
⇒ˆEAH=ˆECB(1)⇒EAH^=ECB^(1) (hai góc có cạnh tương ứng vuông góc)
Có: OA=OE⇒OA=OE⇒ tam giác AOEAOE cân tại OO
⇒ˆAEO=ˆEAO(2)⇒AEO^=EAO^(2)
Chứng minh tương tự ⇒⇒ tam giác EMCEMC cân tại MM
⇒ˆECM=ˆCEM(3)⇒ECM^=CEM^(3)
(1);(2);(3)⇒ˆAEO=ˆCEM(1);(2);(3)⇒AEO^=CEM^
Mà: ˆAEO+ˆOEC=ˆAEC=90∘AEO^+OEC^=AEC^=90∘
⇒ˆOEC+ˆCEM=ˆOEM=90∘⇒OEC^+CEM^=OEM^=90∘
⇒EM⇒EM là tiếp tuyển của (O)(O)

a: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
nên ADHE là tứ giác nội tiếp
hay A,D,H,E cùng thuộc một đường tròn

a: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
Do đó: ADHE là tứ giác nội tiếp
hay A,D,H,E cùng thuộc 1 đường tròn
