Cho tam giác ABC vuông tại A, kẻ phân giác AD. CMR: \(\frac{2}{AD^2}=\frac{1}{DB^2}+\frac{1}{DC^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2020
Mình không biết vẽ hình trên đây bạn tự vẽ hình nhé
a, Xét tam giác BDA và tam giác KDC có: Góc BDA= Góc KDC(đối đỉnh)
Góc B= Góc K(90 độ)
=>Tam giác BDA đồng dạng với tam giác KDC(g.g)
=>\(\frac{DB}{DA}=\frac{DK}{DC}\)
b, Xét tam giác DBK và tam giác DAC có: Góc BDK= Góc DAC(đối đỉnh)
\(\frac{DB}{DA}=\frac{DK}{DC}\)
=>Tam giác DBK đồng dạng với tam giác DAC(c.g.c)
c, Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại B, ta có:
BC2=AC2-AB2
BC2=52-32
BC2=16
BC=4(cm)
Vì AD là phân giác
=>\(\frac{AB}{AC}=\frac{BD}{CD}\)
=>\(\frac{AB}{AC+AB}=\frac{BD}{CD+BD}\)
=>\(\frac{3}{5+3}=\frac{BD}{BC}\)
=>\(\frac{3}{8}=\frac{BD}{4}\)
=>BD=1,5(cm)
=>CD=BC-BD
CD=4-1,5
CD=2,5(cm)
30 tháng 9 2019
Đặt AB = a ; AC = b ; AD = c . Kẻ DE vuông góc AC ( \(E\in AB;F\in AC\) )
Ta có tứ giác AFDE là hình chữ nhật do \(\widehat{A}=\widehat{E}=\widehat{F}=90^o\) , AD phân giác trong của \(\widehat{EAF}\) nên \(\widehat{AFDE}\) là hình vuông . Suy ra
\(DE=DF=\frac{AD\sqrt{2}}{2}=\frac{C\sqrt{2}}{2}\) . Ta có :
\(S_{DAB}+S_{DAC}=S_{ABC}\)
\(\Leftrightarrow\frac{1}{2}AB.DE+\frac{1}{2}DF.AC=\frac{1}{2}AC.AB\)
\(\Leftrightarrow\frac{c\sqrt{2}}{2}a+\frac{c\sqrt{2}}{2}b=ab\)
\(\Leftrightarrow\frac{\sqrt{2}}{c}=\frac{1}{a}+\frac{1}{b}\) . Hay \(\frac{\sqrt{2}}{AD}=\frac{1}{AB}+\frac{1}{AC}\)
Chúc bạn học tốt !!!
CN
0
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
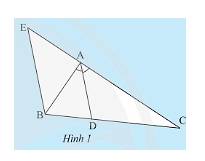
a) Vì \(BE//AD\) nên \(\widehat {EBA} = \widehat {BAD}\) (cặp góc so le trong) (1)
Vì \(BE//AD\) nên \(\widehat {BEA} = \widehat {DAC}\) (cặp góc đồng vị) (2)
Vì \(AD\) là tia phân giác nên \(\widehat {BAD} = \widehat {DAC}\) (tính chất) (3)
Từ (1); (2); (3) suy ra \(\widehat {EBA} = \widehat {AEB}\) (tính chất bắc cầu)
Xét tam giác \(BAE\) có:
\(\widehat {EBA} = \widehat {AEB}\) (chứng minh trên)
Nên tam giác \(BAE\) cân tại \(A\).
b) Vì \(BE//AD\) nên \(\frac{{BD}}{{DC}} = \frac{{AE}}{{AC}}\).
Mà tam giác \(BAE\) cân tại \(A\) nên \(AE = AB \Rightarrow \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (định lí Thales)
Do đó, \(\frac{{DB}}{{DC}} = \frac{{AE}}{{AC}} = \frac{{AB}}{{AC}}\) (điều phải chứng minh).
13 tháng 9 2023
a: AD//BE
=>góc CAD=góc CEB và góc BAD=góc ABE
mà góc CAD=góc BAD
nên góc CEB=góc ABE
=>ΔBAE cân tại A
b: ΔBAE cân tại A
=>AB=AE
=>AB/AC=AE/AC
mà AE/AC=BD/DC(ΔCEB có AD//BE)
nên AB/AC=AE/AC=DB/DC
F
5 tháng 7 2020
Tự vẽ hình chỉ bt làm ý a,c, thôi thông cảm T^T
a,Xét ΔHAB và ΔABC
\(\widehat{BHA}=\widehat{BAH}=90^o\)
Góc B chung
\(\Rightarrow\Delta HBA\text{∼ }\Delta ABC\)
c,Xét ΔABC ta có:
BC2=AC2+AB2
BC2=162+122
BC2=400
BC=√400=20cm
Ta có ΔHAB~ΔABC(câu a)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12.16}{20}=9,6cm\)
5 tháng 7 2020
a.Xét \(\Delta HBA\)và \(\Delta ABC\)có
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{B}\) chung
Do đó \(\Delta HBA\)đồng dạng \(\Delta ABC\)\((\)g.g\()\)
b.Từ \(\Delta HBA\)đồng dạng \(\Delta ABC\)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\)
\(\Rightarrow AH.BC=AB.AC\)
c.Xét \(\Delta ABC\),có \(\widehat{A}\)=90 độ , theo định lý py -ta -go,ta có
\(BC^2=AB^2+AC^2\)
\(BC^2=12^2+16^2\)
\(BC^2=400\)\(\Rightarrow BC=\sqrt{400}\)
\(BC=20cm\)
Ta có \(\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12\times16}{20}\)
\(\Rightarrow AH=9,6cm\)
Chúc bạn học tốt.Phần d mình chưa giải đc nha
۞Ha Ha ð
Bạn phải vẽ hình ra chứ