Một xe A chạy với vận tốc không đổi là vA đuổi theo một chiếc xe B đang chuyển động cùng
hướng với nó với vận tốc 72 km/h trên cùng một đường thẳng. Người lái xe B khi thấy chiếc
xe A còn cách mình 60 m ở phía sau liền tăng tốc với gia tốc không đổi 0, 75 m/s^2 để tránh
sự vượt qua hay sự va chạm với xe A. Biết rằng khoảng cách ngắn nhất khi xe A đến gần xe B
là 6 m. Hãy xác định vận tốc của xe A và thời gian cần thiết để thực hiện điều này ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

28 tháng 11 2019
Gọi mốc thời gian là lúc 2 xe cách nhau 60 m , gốc tọa độ là tại vị trí xe A , chiều dương là chều chuyển động :
\(\hept{\begin{cases}x_A=v_At\\x_B=60+20t+\frac{0,75t^2}{2}\\v_B=20+0,75t\end{cases}}\)
Ta có hệ :
\(\hept{\begin{cases}60+20t+\frac{0,75t^2}{2}-v_At=6\\20+0,75t=v_A\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}t=12\\v_A=29\end{cases}}\)

CX
13 tháng 11 2021
1 ô tô đang chạy với vận tốc 72km/h chậm dần đều với gia tốc 5m/s2
quãng đường ô tô đi được đến khi dừng lại là
72km/h=20m/s
v12-v02=2.a.s⇒⇒s=20m
vậy để không đụng vào chướng ngại vật thì ô tô cần hãm phanh ở vị trí cách chướng ngại vật 1 khoảng ngắn nhất là 20m
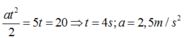
Gọi mốc thời gian là lúc 2 xe cách nhau 60m, gốc toạ độ là tại vị trí xe A, chiều dương là chiều chuyển động:
\(\left\{{}\begin{matrix}x_A=v_At\\x_B=60+20t+\frac{0,75t^2}{2}\\v_B=20+0,75t\end{matrix}\right.\)
Ta có hệ:
\(\left\{{}\begin{matrix}60+20t+\frac{0,75t^2}{2}-v_At=6\\20+0,75t=v_A\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t=12\\v_A=29\end{matrix}\right.\)