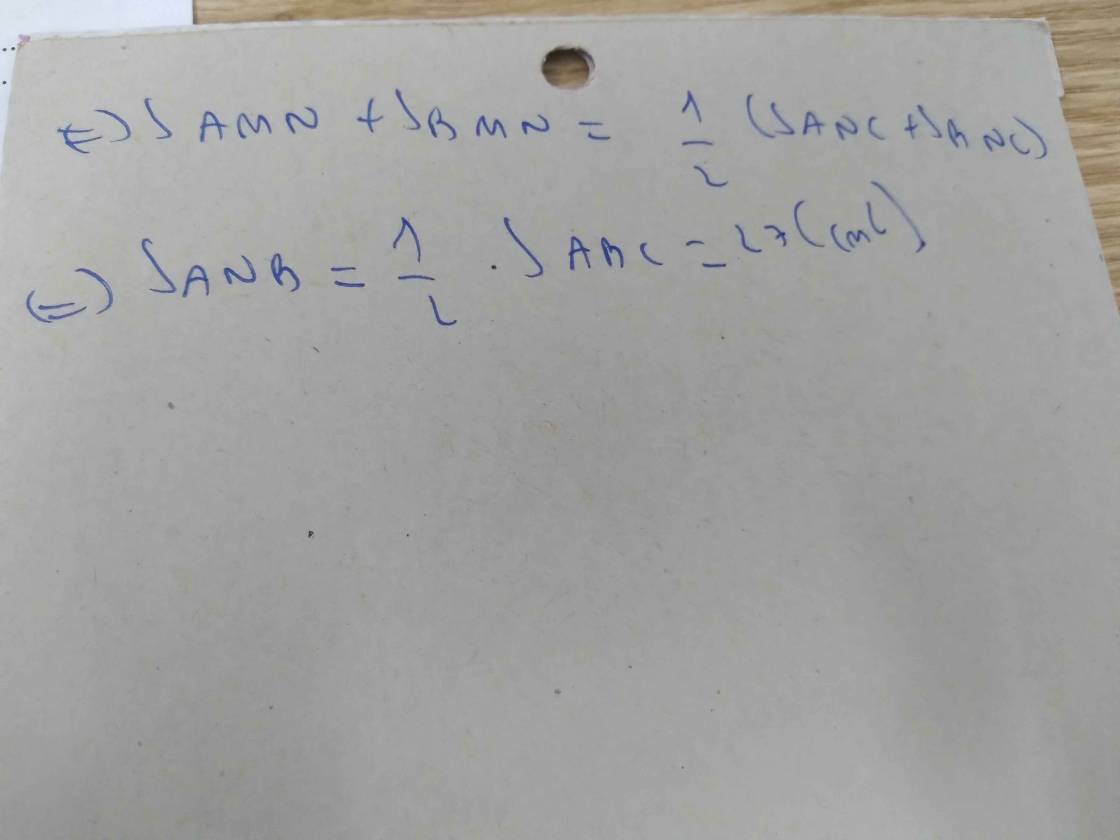Cho một hình tam giác ABC.Trên AB lấy điểm M sao cho AM=1/3 MB.Nối M với C.Trên MC lấy trung điểm N.Nối N với A.Tính diện tích ANC biết diện tích ABC=72 cm vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2023
AM = 1/2 MB => AM = 1/3 AM
=> ACM = 1/3 ABC = 54:3=18cm2
MN = NC
=> ANM=1/2 ACM = 18:2=9cm2
AM = 1/2 MB
=> ANM = 1/2 MNB
=> MNB = 9x2=18cm2
ANB = AMN + MNB = 9+18=27cm2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
24 tháng 5 2022
Hai tg AMC và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow S_{AMC}=\dfrac{1}{3}xS_{ABC}\)
Hai tg AMN và tg AMC có chung đường cao từ A->CM nên
\(\dfrac{S_{AMN}}{S_{AMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{AMN}=\dfrac{1}{2}xS_{AMC}=\dfrac{1}{2}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{6}xS_{ABC}\)
\(S_{BMC}=S_{ABC}-S_{AMC}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)
Hai tg BMN và tg BMC có chung đường cao từ B->MC nên
\(\dfrac{S_{BMN}}{S_{BMC}}=\dfrac{MN}{MC}=\dfrac{1}{2}\Rightarrow S_{BMN}=\dfrac{1}{2}xS_{BMC}=\dfrac{1}{2}x\dfrac{2}{3}xS_{ABC}=\dfrac{1}{3}xS_{ABC}\)
\(S_{ANB}=S_{AMN}+S_{BMN}=\dfrac{1}{6}xS_{ABC}+\dfrac{1}{3}xS_{ABC}=\dfrac{1}{2}xS_{ABC}=40cm^2\)
