Bài 1: Tìm số tự nhiên có năm chữ số, biết rằng nếu viết thêm chữ số 2 vào đằng sau số đó thì được số lớn gấp ba lần số có được bằng cách viết thêm chữ số 2 vào đằng trước số đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
24 tháng 7 2017
Gọi số cần tìm là \(\overline{abcde}\)
Viết chữ số 2 vào đằng sau số đó, ta được số \(\overline{abcde2}\); viết chữ số 2 vào đằng trước số đó, ta được số \(\overline{2abcde}\);
Theo bài ra ta có : \(\overline{abcde2}=3\times\overline{2abcde}\Leftrightarrow10\times\overline{abcde}+2=3\left(200000+\overline{abcde}\right)\)
\(7\times\overline{abcde}=599998\Rightarrow\overline{abcde}=85714\)
Vậy số cần tìm là 85714.
CM
2 tháng 7 2018
Gọi số cần tìm là: a b c d e (a ≠ 0)
Theo bài ra ta có: a b c d e 2 = 3. 2 a b c d e
=> a b c d e .10 + 2 = 3.200000 + 3 a b c d e
=> 7 a b c d e = 599998
=> a b c d e = 85714
Thử lại: 857142 = 3. 285714. Vậy số cần tìm là 857142
MH
9 tháng 9 2021
Gọi số cần tìm là: a b c d e (a ≠ 0)
Theo bài ra ta có: a b c d e 2 = 3. 2 a b c d e
=> a b c d e .10 + 2 = 3.200000 + 3 a b c d e
=> 7 a b c d e = 599998
=> a b c d e = 85714
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
Bài 1:
Số có 5 chữ số có dạng: \(\overline{abcde}\)
Khi viết thêm chữ số 2 vào đằng sau số đó ta được số mới là:
\(\overline{abcde2}\)
Khi viết thêm chữ số 2 vào đằng trước số đó ta được số mới là: \(\overline{2abcde}\)
Theo bài ra ta có: \(\overline{abcde2}\) = \(\overline{2abcde}\) \(\times\) 3
10\(\times\)\(\overline{abcde}\) + 2 = (200000 + \(\overline{abcde}\))\(\times\) 3
\(\overline{abcde}\) \(\times\)10 + 2 = 600000 + \(\overline{abcde}\)\(\times\) 3
\(\overline{abcde}\) \(\times\) 10 - \(\overline{abcde}\) \(\times\) 3 = 600000 - 2
\(\overline{abcde}\) \(\times\) ( 10 - 3) = 599998
7\(a\) = 599998
\(a\) = 599998: 7
\(a\) = 85714
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
Bài 2: Số có hai chữ số có dạng: \(\overline{ab}\)
Khi viết thêm chữ số 1 vào bên trái số và bên phải số đó ta có số mới là: \(\overline{1ab1}\)
Theo bài ra ta có: \(\overline{1ab1}\) = \(\overline{ab}\) \(\times\) 23
1001 + \(\overline{ab}\) \(\times\) 10 = \(\overline{ab}\) \(\times\) 23
\(\overline{ab}\) \(\times\) 23 - \(\overline{ab}\) \(\times\) 10 = 1001
\(\overline{ab}\) \(\times\)(23 - 10) = 1001
\(\overline{ab}\) \(\times\) 13 = 1001
\(\overline{ab}\) = 1001: 13
\(\overline{ab}\) = 77
Kết luận: Số thỏa mãn đề bài là 77
VD
20 tháng 10 2015
gọi số cần tìm là a b c d (a khác 0;a,b,c,d<10)
ta có:2a b c d= a b c d x 5
20000+a b c d= a b c d x 5
=>20000=a b c d x 4(bớt 2 vế đi a b c d)
a b c d=20000:4
a b c d=5000
vậy số cần tìm la 5000
DD
29 tháng 6 2023
Giả sử số tự nhiên có 5 chữ số là ABCDE. Theo đề bài, nếu ta viết thêm chữ số 2 vào đằng sau số đó, ta được số lớn gấp ba lần số ban đầu. Điều này có thể biểu diễn như sau:
ABCDE2 = 3 * 2ABCDE
Để giải phương trình này, ta có thể chia cả hai vế cho 2ABCDE:
(ABCDE2) / (2ABCDE) = 3
Từ đó, ta thấy rằng phần thập phân của phép chia bên trái bằng 3. Vì số tự nhiên có 5 chữ số, nên ABCDE không thể là 0. Do đó, ta có thể loại bỏ trường hợp ABCDE = 0.
Với các giá trị từ 1 đến 9 cho A, B, C, D, E, ta thử từng giá trị và tìm được kết quả duy nhất là:
A = 1, B = 7, C = 8, D = 3, E = 6
Vậy số tự nhiên cần tìm là 17836.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 6 2017
Số cần tìm là abcde số viết thêm là f
=> abcdef = 3.fabcde => 10.abcde + f = 300000.f + 3.abcde
=> 7.abcde = 299999.f => abcde = 42857.f (1)
Do abcde là số có 5 chữ số nên f<3 => f={1;2}
Thay f từng trường hợp vaog 1 đẻ tìm abcde
13 tháng 7 2023
17: Gọi số cần tìm là X
Theo đề, ta có: 1000+10x+1=23X
=>13X=1001
=>X=77
16:
Gọi số cần tìm là X
Theo đề, ta có: \(10X+2=3\left(200000+X\right)\)
=>7X=600000-2=599998
=>X=85714
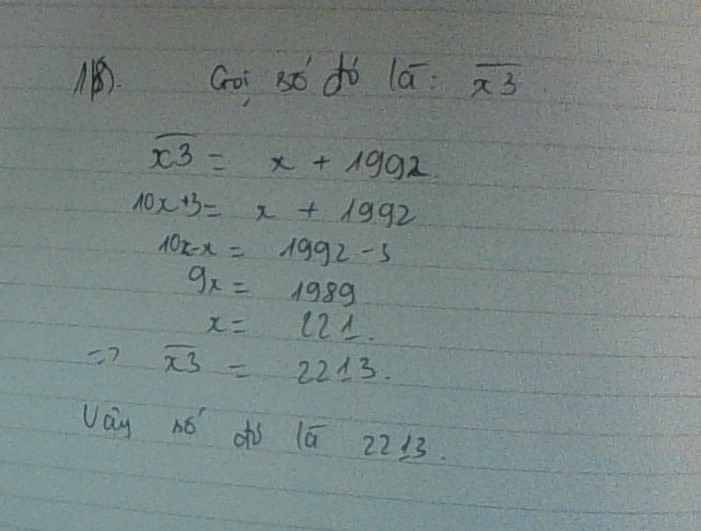
Gọi số có 5 chữ số đó là x (9999<x<100000)
Theo đề bài ta có:
\(\overline{x2}=3\cdot\overline{2x}\)
\(\Leftrightarrow10x+2=3\left(200000+x\right)\)
\(\Leftrightarrow7x=599998\)
\(\Leftrightarrow x=85714\)