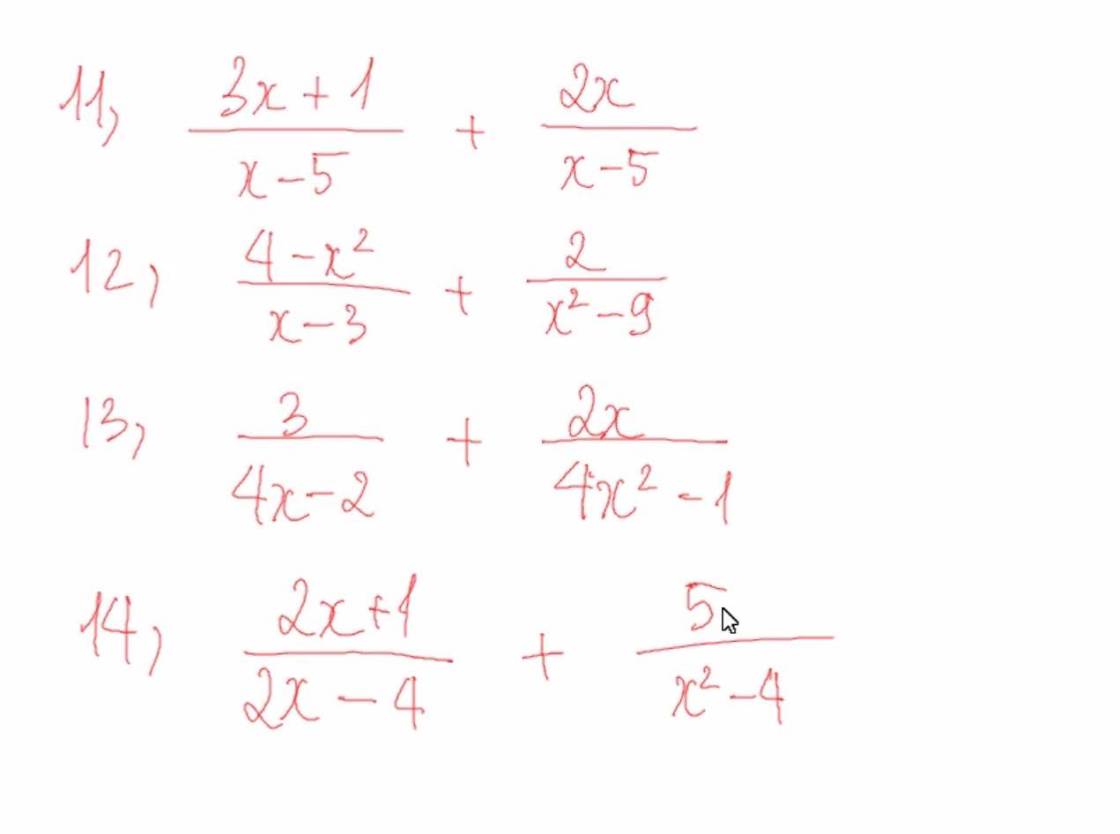
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




- Trong số các đặc điểm chung của Sâu bọ, đặc điểm giúp phân biệt chúng với các Chân khớp khác :
- Cơ thế phân ra thành 3 phần rõ rệt : (đầu, ngực, bụng):
+ Đầu gồm có 1 đôi râu.
+ Ngực gồm có ba đôi chân và hai đôi cánh.
- hô hấp bằng ống khí rất phát triển .

nhấn vào tên của người mình muốn gửi trên phần hỏi đáp có cái mục trò chuyện nhấn vào

\(4-\left|2x+1\right|=3\)
\(\Leftrightarrow\left|2x+1\right|=4-3\)
\(\Leftrightarrow\left|2x+1\right|=1\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=1\\2x+1=-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
Vậy tập ngiệm \(S=\left\{0;-1\right\}\)

\(3n+5⋮n+1\)
\(\Leftrightarrow3\left(n+1\right)+2⋮n+1\)
\(\Leftrightarrow2⋮n+1\)
Vì n là stn => n + 1 > 1
Ta có bảng :
| n + 1 | 1 | 2 |
| n | 0 | 1 |
Vậy \(n\in\left\{0;1\right\}\)

\(Q=-5\cdot\left(-1\right)^2+2\cdot3+2021=2027-5=2022\)

Cảm ơn em đã tin tưởng và lựa chọn đồng hành cùng olm.
Olm là môi trường an toàn, lành mạnh, thân thiện, tích cực là nơi để chia sẻ kiến thức và lan tỏa yêu thương, tương trợ, giúp đỡ tới tất cả mọi người, nên em sẽ nhận được những điều đó từ cộng đồng tri thức olm em nhé

11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)

Để ( 2x - 1/2 ) ( 3x - 1/3 ) < 0 thì xảy ra 2 trường hợp :
TH1 : 2x - 1/2 > 0 và 3x - 1/3 < 0
\(\Rightarrow\hept{\begin{cases}2x-\frac{1}{2}>0\\3x-\frac{1}{3}< 0\end{cases}\Rightarrow\hept{\begin{cases}x>\frac{1}{4}\\x< \frac{1}{9}\end{cases}\Rightarrow}x\in\varnothing}\)
TH2 : 2x - 1/2 < 0 và 3x - 1/3 > 0
\(\Rightarrow\hept{\begin{cases}2x-\frac{1}{2}< 0\\3x-\frac{1}{3}>0\end{cases}\Rightarrow\hept{\begin{cases}x< \frac{1}{4}\\x>\frac{1}{9}\end{cases}\Rightarrow\frac{1}{9}< x< \frac{1}{4}}}\)
Vậy,...........