Một electron chuyển động dọc theo một đường sức của điện trường đều có cường độ 182 V/m. Electron xuất phát từ điểm O với vận tốc 3200 km/s. Vectơ vận tốc\(\overrightarrow{v}\) cùng hướng với đường sức điện. Sau bao lâu kể từ lúc xuất phát, electron lại trở về điểm O?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
22 tháng 3 2017
Chọn đáp án C
@ Lời giải:
+ Khi electron chuyển động theo hướng của véc tơ E thì lực F đòng vai trò là lực cản
+ Gọi s là quãng đường electron đi được đến khi dừng lại (v = 0)
Công của lực điện trường: A = q.E.s = e.E.s
+ Áp dụng định lý biến thiên động năng ta có:
LT
1 tháng 4 2019
Đáp án C.
A = |q|.E.d = | ∆ W đ | = 1 2 m v 2
ð d = m v 2 2. | q | . E = 9 , 1.10 − 31 . ( 3.10 5 ) 2 2.1 , 6.10 − 19 .100 = 25 , 6 . 10 - 4 m.
VT
1 tháng 2 2019
Đáp án A
Lúc đầu,chuyển động chậm dần đều và dừng lại ở điểm O,sau đó đổi chiều chuyển động và chuyển động nhanh dần đều trở về M
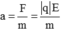
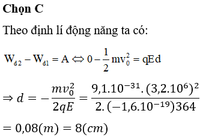
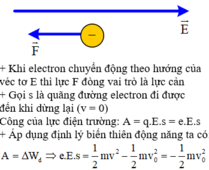
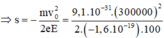
Để giải bài tập này thì em chú ý đến hiện tượng như sau: Ban đầu thì điện tích chuyển động với vận tốc v cùng hướng với đường sức và lúc này electron chịu tác dụng của lực điện ngược chiều điện trường => Đến vị trí A nào đó điện tích sẽ có vận tốc = 0. Và lực điện kéo điện tích lại vị trí ban đầu O.
Gai đoạn 1 (O-A): AD Định lí biến thiên động năng:
\(\frac{1}{2}mv^2_2-\frac{1}{2}mv^2=A_F=qEd\)
\(\Rightarrow0-\frac{1}{2}mv^2=-1,6.10^{-19}.182.d\Rightarrow d=0,16m\) với \(m_e=9,1.10^{-31}kg;v=3200000\)m/s.
\(v^2-v_1^2=2aS\Rightarrow a=0^2-\frac{\left(32.10^5\right)^2}{2S}=-3,8.10^{13}\) m/s^2
\(\Rightarrow v=v_0+at\Rightarrow t=8,42.10^8s\)
Giai đoạn 2(A-O): Tương tự \(t_2=t_1\)
Vậy thời gian để e trở lại vị trí ban đầu là \(t=1,68.10^7s\)