cho hàm số y=(k+1)x+k-1 ( với k là tham số)
chứng tỏ đồ thị hàm số luôn đi qua 1 điểm cố định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


CHO hàm số y=2k+ (k+1)
điều kiện hàm số là bậc nhất là \(2k\ne0\Leftrightarrow k\ne0\)
biết đò thị đii qua điểm M (1;4)
=> 4=2k+k+1
<=> 4=3k+1
<=> k=1
vậy k=1 thì đồ thị hàm số là y=2x+2
Gỉa sử đồ thị hàm số y = 2kx + (k + 1) luôn đi qua 1 điểm cố định M(x0;y0)
=> x = x0 ; y = y0
Thay x = x0 ; y = y0 vào đồ thị hàm số trên ta được:
\(y_0=2kx_0+\left(k+1\right)\)
\(\Rightarrow2kx_0+k+1-y_0=0\)
\(\Rightarrow k\left(2x_0+1\right)+1-y_0=0\)
\(\Rightarrow\hept{\begin{cases}2x_0+1=0\\1-y_0=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x_0=\frac{-1}{2}\\y_0=1\end{cases}}\)
\(\Rightarrow M\left(\frac{-1}{2};1\right)\)
Vậy......

Câu a :))
Hàm số đã cho đồng biến .
giải thích :
Do \(m^2\ge0\forall m\)
\(\Rightarrow m^2+1>0\)
Vậy hàm số trên đồng biến.
Giả sử đths đi qua điểm cố định ( x0;y0 )
Ta có y0 = ( m2 +1 )x0 - 1
<=> y0 = m2 x0 +x0 -1
<=> y0 -x0 +1 -m2x0 = 0
Để pt nghiệm đúng với mọi m \(\Leftrightarrow\hept{\begin{cases}y_0-x_0+1=0\\x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}y_0=-1\\x_0=0\end{cases}}}\)
Vậy đths luôn đi qua điểm cố định ( 0 ; -1 )

\(a,\Leftrightarrow k-2\ne0\Leftrightarrow k\ne2\\ b,\text{Đồng biến }\Leftrightarrow k-2>0\Leftrightarrow k>2\\ \text{Nghịch biến }\Leftrightarrow k-2< 0\Leftrightarrow k< 2\\ c,\Leftrightarrow x=0;y=0\Leftrightarrow k=0\\ d,\Leftrightarrow-\left(k-2\right)+k=2\Leftrightarrow0k+2=2\Leftrightarrow k\in R\)

Thay x=1 và y=4 vào y=kx+1, ta được:
k+1=4
=>k=3
=>y=3x+1
=>Hàm số đồng biến

Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o , y o ).
Ta có:
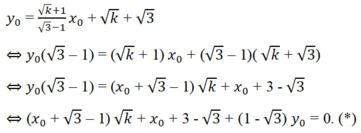
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:
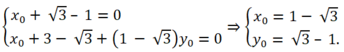
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1- 3 ; 3 – 1).