Xác định m để phương trình : \(\dfrac{2}{x+1}-\dfrac{m}{x-2}=0\) có nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
2 tháng 4 2023
\(x^2-x+1-m=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=1-m\end{matrix}\right.\)
Ta có :
\(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)
\(\Leftrightarrow5\left(\dfrac{x_2+x_1}{x_1x_2}\right)-x_1x_2+4=0\)
\(\Leftrightarrow5\left(\dfrac{1}{1-m}\right)-\left(1-m\right)+4=0\)
\(\Leftrightarrow\dfrac{5}{1-m}-1+m+4=0\)
\(\Leftrightarrow\dfrac{5}{1-m}+m+3=0\)
\(\Leftrightarrow\dfrac{5+m\left(1-m\right)+3\left(1-m\right)}{1-m}=0\)
\(\Leftrightarrow5+m-m^2+3-3m=0\)
\(\Leftrightarrow-m^2-2m+8=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)
QB
10 tháng 4 2021
x2-2(m-1)x+m2-3m=0
△'=[-(m-1)]2-1(m2-3m)=(m-1)2-(m2-3m)=m2-2m+1-m2+3m= m+1
áp dụng hệ thức Vi-ét ta được
x1+x2=2(m-1) (1)
x1*x2=m2-3m (2)
a) để PT có 2 nghiệm phân biệt khi m+1>0 <=> m>-1
b) để PT có duy nhất một nghiệm âm thì x1*x2 <0
10 tháng 4 2021
e) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1x_2=m^2-3m\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\)
\(\Leftrightarrow\left(2m-2\right)^2-2\cdot\left(m^2-3m\right)-8=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+6m-8=0\)
\(\Leftrightarrow2m^2-2m-4=0\)(1)
\(\Delta=\left(-2\right)^2-4\cdot2\cdot\left(-4\right)=4+32=36\)
Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{2-\sqrt{36}}{4}=\dfrac{2-6}{4}=-1\\m_2=\dfrac{2+\sqrt{36}}{4}=\dfrac{2+6}{4}=2\end{matrix}\right.\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2=8\) thì \(m\in\left\{-1;2\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1
Đặt \(cosx=t\in\left[-1;1\right]\)
\(\Rightarrow6t^2+\left(9m-7\right)t-6m+2=0\)
\(\Leftrightarrow6t^2-7t+2+9mt-6m=0\)
\(\Leftrightarrow\left(2t-1\right)\left(3t-2\right)+3m\left(3t-2\right)=0\)
\(\Leftrightarrow\left(3t-2\right)\left(2t+3m-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{2}{3}\\cosx=\dfrac{-3m+1}{2}\end{matrix}\right.\)
(Chà tới đây mới thấy ko cần đặt ẩn phụ, nhìn con số 9m và 6m to 1 cách vô lý đã nghi nghi có gì đó bất thường trong nghiệm :D)
Pt \(cosx=\dfrac{2}{3}\) cho 1 nghiệm thuộc \(\left(0;\dfrac{\pi}{2}\right)\)
Để pt có 3 nghiệm pb thì \(cosx=\dfrac{-3m+1}{2}\) cho 2 nghiệm pb thuộc khoảng đã cho
Từ đường tròn lượng giác ta dễ dàng suy ra: \(-1< \dfrac{-2m+1}{2}< 0\)
3 tháng 3 2022
Trường hợp 1: m=10
Phương trình sẽ là -40x+6=0
hay x=3/20
=>m=10 sẽ thỏa mãn trường hợp a
Trường hợp 2: m<>10
\(\Delta=\left(-4m\right)^2-4\left(m-10\right)\left(m-4\right)\)
\(=16m^2-4\left(m^2-14m+40\right)\)
\(=16m^2-4m^2+56m-160\)
\(=12m^2+56m-160\)
\(=4\left(3m^2+14m-40\right)\)
\(=4\left(3m^2-6m+20m-40\right)\)
\(=4\left(m-2\right)\left(3m+20\right)\)
a: Để phương trình có nghiệm thì (m-2)(3m+20)>=0
=>m>=2 hoặc m<=-20/3
b: Để phương trình có hai nghiệm phân biệt đều dương thì
\(\left\{{}\begin{matrix}\left(m-2\right)\left(3m+20\right)>0\\\dfrac{4m}{m-10}>0\\\dfrac{m-4}{m-10}>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left(m-2\right)\left(3m+20\right)>0\\m\in\left(-\infty;0\right)\cup\left(10;+\infty\right)\\m\in\left(-\infty;4\right)\cup\left(10;+\infty\right)\end{matrix}\right.\)
\(\Leftrightarrow m\in\left(-\infty;-\dfrac{20}{3}\right)\cup\left(10;+\infty\right)\)
22 tháng 5 2023
a) Khi $a=3$, ta có phương trình:
$$x-3x+3-x+3x-3+3^2+3^3-3^2=0$$
$$\Leftrightarrow 6x=51 \Leftrightarrow x=\frac{17}{2}$$
Vậy nghiệm của phương trình là $x=\frac{17}{2}$.
b) Khi $a=1$, ta có phương trình:
$$x-x+1-x+1x-1+3+1-1=0$$
$$\Leftrightarrow x=0$$
Vậy nghiệm của phương trình là $x=0$.
c) Để phương trình có nghiệm $x=0,5$, ta cần giải phương trình:
$$0,5-a(0,5)+a-0,5+a(0,5)-a+3a^2+a^3-a^2=0$$
$$\Leftrightarrow a^3+3a^2-2a=0$$
$$\Leftrightarrow a(a-1)(a+2)=0$$
Vậy các giá trị của $a$ để phương trình có nghiệm $x=0,5$ là $a=0,1$ hoặc $a=-2$.
PT
1
10 tháng 2 2022
\(\Leftrightarrow\left(4-m\right)\left(m+1\right)=2\)
\(\Leftrightarrow4m+4-m^2-m-2=0\)
\(\Leftrightarrow-m^2+3m+2=0\)
\(\Leftrightarrow m^2-3m-2=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{3-\sqrt{17}}{2}\\m_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)
3 tháng 4 2022
\(x^2-x+1-m=0\left(1\right)\\ \text{PT có 2 nghiệm }x_1,x_2\\ \Leftrightarrow\Delta=1-4\left(1-m\right)\ge0\\ \Leftrightarrow4m-3\ge0\Leftrightarrow m\ge\dfrac{3}{4}\\ \text{Vi-ét: }\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=1-m\end{matrix}\right.\\ \text{Ta có }5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\\ \Leftrightarrow5\cdot\dfrac{x_1+x_2}{x_1x_2}-x_1x_2+4=0\\ \Leftrightarrow\dfrac{5}{1-m}+m-1+4=0\\ \Leftrightarrow\dfrac{5}{1-m}+m+3=0\\ \Leftrightarrow5+\left(1-m\right)\left(m+3\right)=0\\ \Leftrightarrow m^2+2m-8=0\\ \Leftrightarrow m^2-2m+4m-8=0\\ \Leftrightarrow\left(m-2\right)\left(m+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(n\right)\\m=-4\left(l\right)\end{matrix}\right.\)
Vậy $m=2$
9 tháng 5 2020
x2 - 2(m - 1)x +m2 + 4m + 13 = 0 (1) \(\left(a=1;b=-2\left(m-1\right);c=m^2+4m+13\right)\)
Ta có \(\Delta'=\left(-\left(m-1\right)\right)^2-1.\left(m^2+4m+13\right)\)
\(=m^2-2m+1-m^2-4m-13\)
\(=-6m-12=-6\left(m+2\right)\)
a+b, Để phương trình (1) có nghiệm \(\Leftrightarrow\Delta'\ge0\Leftrightarrow-6\left(m+2\right)\ge0\)
\(\Leftrightarrow m+2\le0\)
\(\Leftrightarrow m\le-2\)
Câu b giống với câu a nhé!
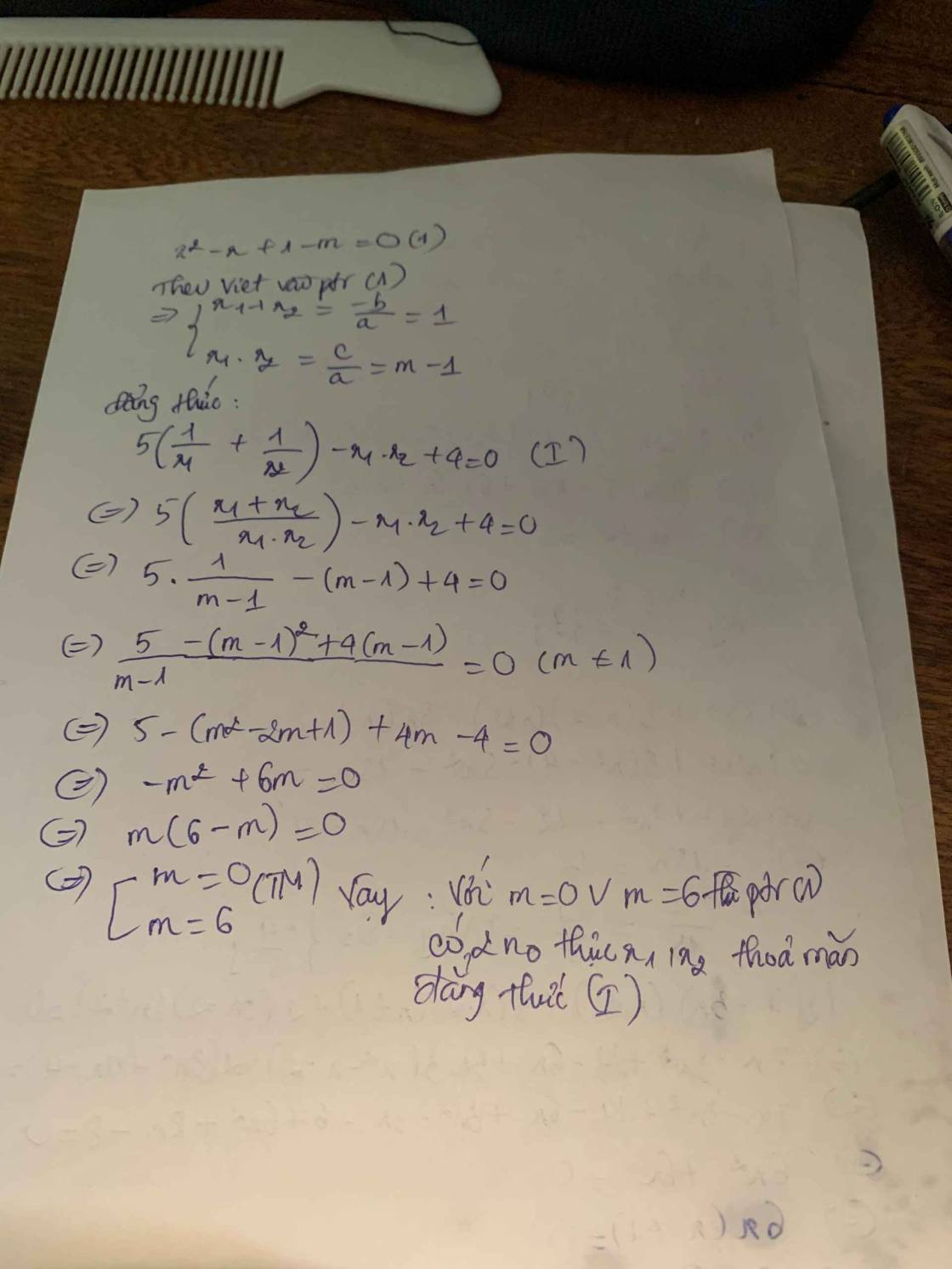
`2/(x+1)-m/(x-2)=0(x\ne-1,x\ne2)`
`<=>2/(x+1)=m/(x-2)`
`<=>2(x-2)=m(x+1)`
`<=>2x-4=mx+m`
`<=>mx-2x=-m-4`
`<=>x(m-2)=-4-m`
Để pt có nghiệm
`=>m-2ne0=>m ne 2`
`=>x=(-4-m)/(m-2)`
`x ne -1=>(-4-m)/(m-2)\ne-1`
`=>(-m-4)/(m-2)+1\ne0`
`<=>-2/(m-2) ne 0` luôn đúng với m khác 2
`x ne 2=>(-4-m)/(m-2)\ne2`
`=>(-m-4)/(m-2)-2 \ne 0`
`=>(-3m-8)/(m-2)\ne0`
`=>-3m-8\ne0`
`=>m\ne-8/3`
Vậy với `m ne 2` và `m ne -8/3` thì pt có nghiệm
Đk: \(\left\{{}\begin{matrix}x+1\ne0\\x-2\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne2\end{matrix}\right.\)
Pt: \(\Rightarrow2\left(x-2\right)-m\left(x+1\right)=0\)
\(\Rightarrow2x-4-mx-m=0\) \(\Rightarrow x\left(2-m\right)=m+4\)
\(\Rightarrow x=\dfrac{m+4}{2-m}\)
Mà \(x\ne-1vàx\ne2\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{m+4}{2-m}\ne-1\\\dfrac{m+4}{2-m}\ne2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4\ne-2\left(luônđúng\right)\\m\ne0\end{matrix}\right.\)
Vậy với \(m\ne0\) thì pt có nghiệm.