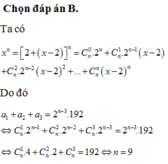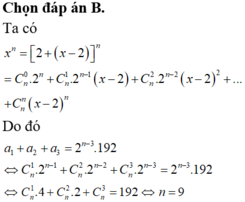Tìm x,n nguyên dương để xn+1 + 2n+1 + 1 \(⋮\)xn + 2n +1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2019
Chọn B.
Phương pháp:
Cách giải: Ta có:
x n + 1 = x n 2 ( 2 n + 1 ) x n + 1
⇔ 1 x n + 1 = 2 ( 2 n + 1 ) + 1 x n
Đặt u n = 1 x n
ta có: u n + 1 = 2 ( 2 n + 1 ) + u n
Vậy u 100 = 2 ( 2 . 99 + 1 ) + 2 ( 2 . 98 + 1 ) + . . . 2 ( 2 . 1 + 1 ) + 3 2
⇒ = 39999 2
Vậy x 100 = 39999 2
CM
2 tháng 9 2019
Chọn A.
Ta có: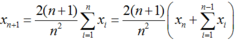 
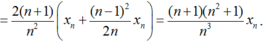
Do đó: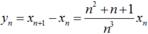 
- Ta chứng minh dãy (yn) tăng.
Ta có: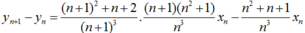 
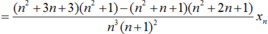
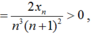
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
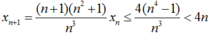
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: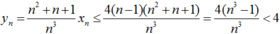 
Vậy bài toán được chứng minh.
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
AH
Akai Haruma
Giáo viên
21 tháng 1 2022
Lời giảiL
$A=1+x+x^2+...+x^n$
$xA=x+x^2+x^3+...+x^n+x^{n+1}$
$\Rightarrow xA-A=(x+x^2+x^3+...+x^{n+1})-(1+x+x^2+...+x^n)$
Hay $A(x-1)=x^{n+1}-1$
$\Rightarrow A=\frac{x^{n+1}-1}{x-1}$ với $x$ nguyên dương khác $1$
Vì $A$ nguyên với mọi $x$ nguyên dương, $n$ tự nhiên nên $\frac{x^{n+1}-1}{x-1}$ nguyên
$\Rightarrow x^{n+1}-1\vdots x-1$ (đpcm)
