cho Bx // Ny // Oz, \(\widehat{OBx}\)=130\(^0\)và \(\widehat{ONy}\)=140\(^0\). tính \(\widehat{BON}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


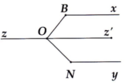 Kẻ Oz' là tia đối của tia Oz.
Kẻ Oz' là tia đối của tia Oz.
Ta có: Bx //Oz => x B O ^ + B O z ' ^ = 180°
=> B O z ' ^ = 50°.
Oz// Ny => z ' O N ^ + O N y ^ = 180°
=> z ' O N ^ = 40 ° = > B O N ^ = 50°+ 40° = 90°.

Do Bx // Oz => góc BOz' = góc xBO = 180o (Do 2 góc trong cùng phía)
mà góc xBO = 130o
=> góc BOz' + 130o = 180o
=> góc BOz' = 180o - 130o= 50o
Do Oz // Ny mà Oz' là tia đối của tia Oz => Oz' // Ny
=> z'ON + ONy = 180o ( do 2 góc trong cùng phía)
mà góc ONy = 140o
=> z'ON + 140o = 180o
=> z'ON = 180o - 140o = 40o
Ta thấy: góc BON = góc BOz' + z'ON = 50o + 40o = 90o
Vậy góc BON= 90o


a) vì \(\widehat{xOy}>\widehat{xOz}\) nên tia Oz là tia nằm giữa 2 tia còn lại .
b) \(\widehat{yOz}=\widehat{xOy}-\widehat{xOz}\)
\(\widehat{yOz}=130^o-65^o\)
\(\widehat{yOz}=65^o\)
Vậy \(\widehat{xOz}=\widehat{yOz}\left(60^o=60^o\right)\)
c) Tia Oz là tia phân giác của \(\widehat{xOy}\) . Vì \(\widehat{xOz}=\widehat{yOz}=\frac{\widehat{xOy}}{2}=\frac{130^o}{2}=65^o\) , nên tia Oz là tia phân giác của \(\widehat{xOy}\)

Bài làm
Bài 1:
a) Trên nửa mặt phẳng có bờ chứa tia Ox có:
OB > OM ( 4 cm > 1 cm )
=> M nằm giữa hai điểm B và O
Ta có: OM + BM = OB
Hay 1 + BM = 4
=> BM = 4 - 1 = 3
Lại có: MO + OA = MA
Hay 1 + 2 = MA
=> MA = 3
Mà BM = 3
=> MA = BM ( 3cm = 3cm )
=> M là trung điểm của AB.
b) Trên nửa mặt phẳng có bờ chứa tia Oy có:
^zOy < ^tOy ( 30° < 130° )
=> Oz nằm giữa hai tia Ot và Oy.
Ta có: ^tOz + ^zOy = ^tOy
Hay ^tOz + 30° = 130°
=> ^tOz = 130° - 30° = 100°

b) Ta có: tia Oz nằm giữa hai tia Ox và Ot(cmt)
nên \(\widehat{xOz}+\widehat{tOz}=\widehat{xOt}\)
\(\Leftrightarrow\widehat{tOz}+70^0=125^0\)
hay \(\widehat{tOz}=55^0\)
Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow70^0+\widehat{yOz}=180^0\)
hay \(\widehat{yOz}=110^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOt}< \widehat{yOz}\left(55^0< 110^0\right)\)
nên tia Ot nằm giữa hai tia Oy và Oz
Ta có: tia Ot nằm giữa hai tia Oy và Oz(cmt)
mà \(\widehat{yOt}=\widehat{zOt}\left(=55^0\right)\)
nên Ot là tia phân giác của \(\widehat{yOz}\)(đpcm)
a) Ta có: \(\widehat{yOt}+\widehat{xOt}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xOt}+55^0=180^0\)
hay \(\widehat{xOt}=125^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOt}\left(70^0< 125^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Ot(Đpcm)
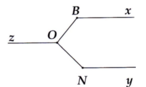
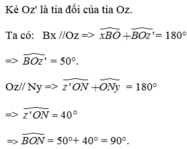
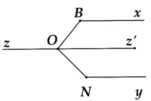
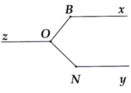

Ta có: ^OBx + ^BOz = 1800 ( trong cùng phía của Bx // Oz)
=> ^BOz = 1800 - ^BOx = 1800 - 1300 = 500
^zON + ^ONy = 1800 (trong cùng phía của Oz // Ny)
=> ^zOn = 1800 - ^ONy = 1800 - 1400 = 400
Vậy: ^BON = ^BOz + ^zOn = 500 + 400 = 900
bạn giúp mk cách vẽ hình với