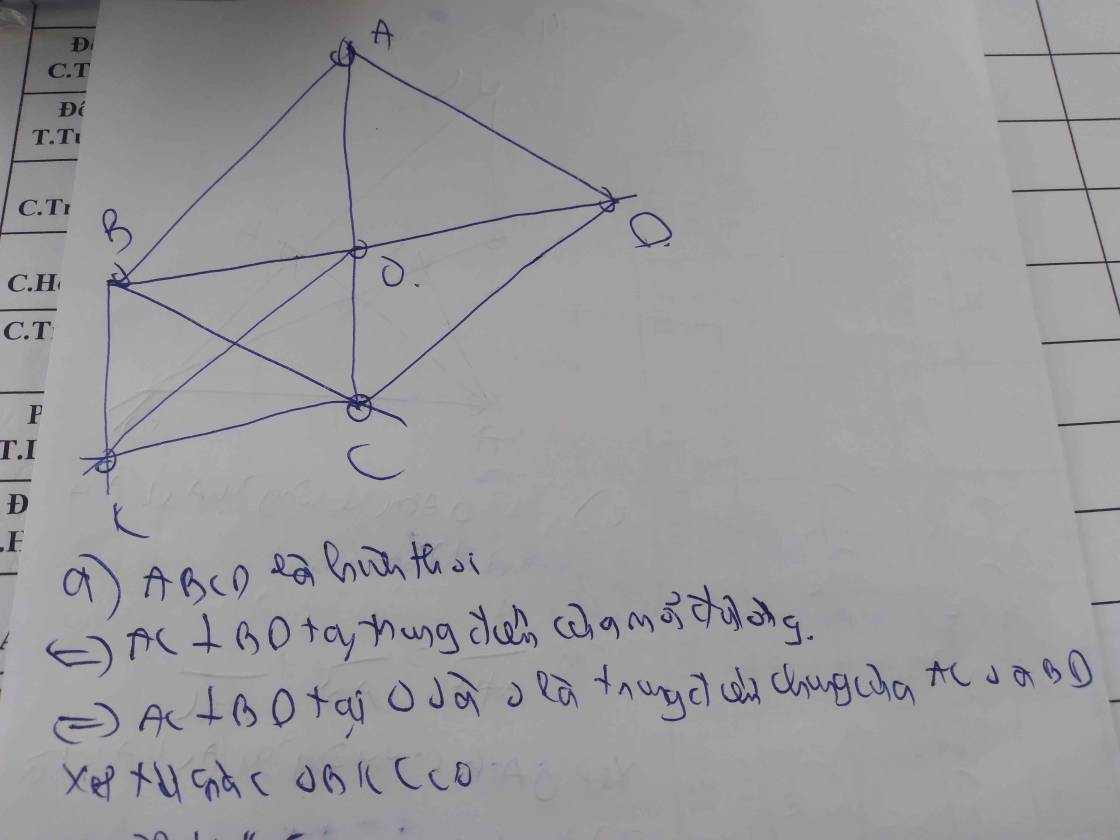
Cho hthoi ABCD , O là giao điểm của 2 đường chéo AC và BD . Qua B vẽ đường thẳng //AC , qua C kẻ đường thẳng// BD chúng cắt nhau tại I
a, Cm OBIC là hcn?
b, Cm AB=OI ?
c, Tìm điều kiện của hthoi ABCD để tứ giác OBIC là hình vuông ?
( Kẻ hình giùm mk ạ )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 11 2017
có BI//AC gt / CI//BD BOC=90 độ (tcht) suy ra tứ giác OBIC LÀ hình chữ nhật dkpcm
có OBIC là hình chữ nhật suy ra OI=BC (tchcn) mà BC = AB suy ra OIBAB dkpcm
hình thoi abcd cần có 1 góc vuông hình chữ nhất OIBAB là hình vuông
CW
27 tháng 11 2016
Đây chỉ là hướng giải, ko phải bài giải nhé ^^!
a) Chứng minh theo dấu hiệu hình hình hành có 1 góc vuông là hcn
b) Cm theo DH Tứ giác có 2 cạnh đối song song và bằng nhau là hình bình hành => AB = OI (2 cạnh đối)
c) Để OBIC là hình vuông thì OB = OC hay BD = AC <=> ABCD là hình vuông
18 tháng 10 2023
a: ABCD là hình thoi
=>AC vuông góc BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
Xét tứ giác OBKC có
OB//KC
OC//BK
Do đó: OBKC là hình bình hành
mà \(\widehat{BOC}=90^0\)
nên OBKC là hình chữ nhật
b: OBKC là hình chữ nhật
=>OK=BC
mà BC=AB
nên OK=AB
c: Để OBKC là hình vuông thì OB=OC
mà \(OB=\dfrac{BD}{2};OC=\dfrac{AC}{2}\)
nên BD=AC
GT
24 tháng 12 2019
Hình vẽ và giả thiết tụ vẽ nhé+)
a) Có ABCD là hình thoi
⇒ BD ⊥ AC tại O ⇒ \(\widehat{BOC}\)= 90o
Có: BK ⊥ AC (gt)
BD ⊥ AC
=> BD ⊥ BK => \(\widehat{DBK} \) = 90o
Có: KC // BD (gt)
BD ⊥ AC
=> KC ⊥ AC => \(\widehat{OCK}\) = 90o
Xét tứ giác OBKC có:
\(\widehat{BOK} = \widehat{OBK} = \widehat{OCK} = 90\)o
=> tứ giác OBKC là hình chữ nhật
b) có tứ giác OBKC là hình chữ nhật ( ý a )
=> OK = BC
mà BC = AB ( tính chất hình thoi )
=> AB = OK
c) Để được OBKC là hình vuông
<=> OB = OC ( 2 cạnh kề nhau )
OB = \(\frac{1}{2}\) BD
OC = \(\frac{1}{2}\) AC
=> AC = BD
=> ABCD là hình vuông
Vậy hình thoi ABCD là hình vuông thì OBKC là hình vuông
