Tìm GTNN của biểu thức
P = x2 - 6x + y2 - 2y + 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1P
1
16 tháng 10 2021
\(P=\left(x^2-6x+9\right)+\left(y^2-2y+1\right)+2\\ P=\left(x-3\right)^2+\left(y-1\right)^2+2\ge2\\ P_{min}=2\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
5 tháng 3 2022
a, xem lại đề
\(b,x^2-4x+y^2-6y+1\\ =\left(x^2-4x+4\right)+\left(y^2-6y+9\right)-12\\ =\left(x-2\right)^2+\left(y-3\right)^2-12\ge-12\)
Dấu "=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
Vậy ...
\(c,x^2-4xy+5y^2-2y+5\\ =\left(x^2-4xy+4y^2\right)+\left(y^2-2y+1\right)+4\\ =\left(x-2y\right)^2+\left(y-1\right)^2+4\ge4\)
Dấu "=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy ...
5 tháng 3 2022
a,
b,x2−4x+y2−6y+1=(x2−4x+4)+(y2−6y+9)−12=(x−2)2+(y−3)2−12≥−12b,x2−4x+y2−6y+1=(x2−4x+4)+(y2−6y+9)−12=(x−2)2+(y−3)2−12≥−12
Dấu "=" xảy ra⇔{x=2y=3⇔{x=2y=3
Vậy ...
c,x2−4xy+5y2−2y+5=(x2−4xy+4y2)+(y2−2y+1)+4=(x−2y)2+(y−1)2+4≥4c,x2−4xy+5y2−2y+5=(x2−4xy+4y2)+(y2−2y+1)+4=(x−2y)2+(y−1)2+4≥4
Dấu "=" xảy ra⇔{x=2y=1⇔{x=2y=1
Vậy ...
19 tháng 12 2020
A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
19 tháng 12 2020
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
HQ
Hà Quang Minh
Giáo viên
9 tháng 8 2023
\(a,M=x^2-4x+5=\left(x-2\right)^2+5\\ \Rightarrow M\ge5\)
Dấu "=" xảy ra \(\Leftrightarrow x=2\)
\(b,N=y^2-y-3=\left(y-\dfrac{1}{2}\right)^2-\dfrac{13}{4}\\ \Rightarrow N\ge-\dfrac{13}{4} \)
Dấu "=" xảy ra \(\Leftrightarrow y=\dfrac{1}{2}\)
\(P=x^2+y^2-4x+y+7=\left(x-2\right)^2+\left(y+\dfrac{1}{2}\right)^2+\dfrac{11}{4}\\ \Rightarrow P\ge\dfrac{11}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\)
9 tháng 8 2023
a: M=x^2-4x+4+1
=(x-2)^2+1>=1
Dấu = xảy ra khi x=2
b: N=y^2-y+1/4-13/4
=(y-1/2)^2-13/4>=-13/4
Dấu = xảy ra khi y=1/2
c: P=x^2-4x+4+y^2+y+1/4+11/4
=(x-2)^2+(y+1/2)^2+11/4>=11/4
Dấu = xảy ra khi x=2 và y=-1/2
27 tháng 8 2021
`A=2x^2-2xy-6x+y^2+10`
`A=x^2-2xy+y^2+x^2-6x+10`
`A=(x-y)^2+x^2-6x+9+1`
`A=(x-y)^2+(x-3)^2+1`
Vì `(x-y)^2+(x-3)^2>=0=>A>=1`
Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`
TH
2
T
16 tháng 10 2023
\(B=y^2-y+1\)
\(=y^2-2\cdot y\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\dfrac{1}{4}+1\)
\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Ta thấy: \(\left(y-\dfrac{1}{2}\right)^2\ge0\forall y\)
\(\Rightarrow\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)
Dấu \("="\) xảy ra \(\Leftrightarrow y-\dfrac{1}{2}=0\Leftrightarrow y=\dfrac{1}{2}\)
Vậy \(B_{min}=\dfrac{3}{4}\) khi \(y=\dfrac{1}{2}\).
\(---\)
\(C=x^2-4x+y^2-y+5\)
\(=\left(x^2-4x+4\right)+\left(y^2-y+\dfrac{1}{4}\right)+\dfrac{3}{4}\)
\(=\left(x^2-2\cdot x\cdot2+2^2\right)+\left[y^2-2\cdot y\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]+\dfrac{3}{4}\)
\(=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Ta thấy: \(\left(x-2\right)^2\ge0\forall x\)
\(\left(y-\dfrac{1}{2}\right)^2\ge0\forall y\)
\(\Rightarrow\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2\ge0\forall x;y\)
\(\Rightarrow\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x;y\)
Dấu \("="\) xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(C_{min}=\dfrac{3}{4}\) khi \(x=2;y=\dfrac{1}{2}\).
\(Toru\)
MH
16 tháng 10 2023
\(B=y^2-y+1\)
\(=y^2-2.y.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Vì \(\left(y-\dfrac{1}{2}\right)^2\ge0\forall y\Rightarrow B\ge\dfrac{3}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow y=\dfrac{1}{2}\)
\(C=x^2-4x+y^2-y+5\)
\(=x^2-4x+4+y^2-y+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2\)
Vì \(\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2\ge0\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
17 tháng 6 2021
\(a,-x^2+2x+5=-\left(x^2-2x-5\right)=-\left(x^2-2x+1-6\right)=-\left(x-1\right)^2+6\le6\)
dấu'=' xảy ra<=>x=1=>Max A=6
\(b,B=-x^2-y^2+4x+4y+2=-x^2+4x-4-y^2+4x-4+10\)
\(=-\left(x^2-4x+4\right)-\left(y^2-4x+4\right)+10\)
\(=-\left(x-2\right)^2-\left(y-2\right)^2+10=-\left[\left(x-2\right)^2+\left(y-2\right)^2\right]+10\le10\)
dấu"=" xảy ra<=>x=y=2=>Max B=10
\(c,C=x^2+y^2-2x+6y+12=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\)
dấu'=' xảy ra<=>x=1,y=-3=>MinC=2
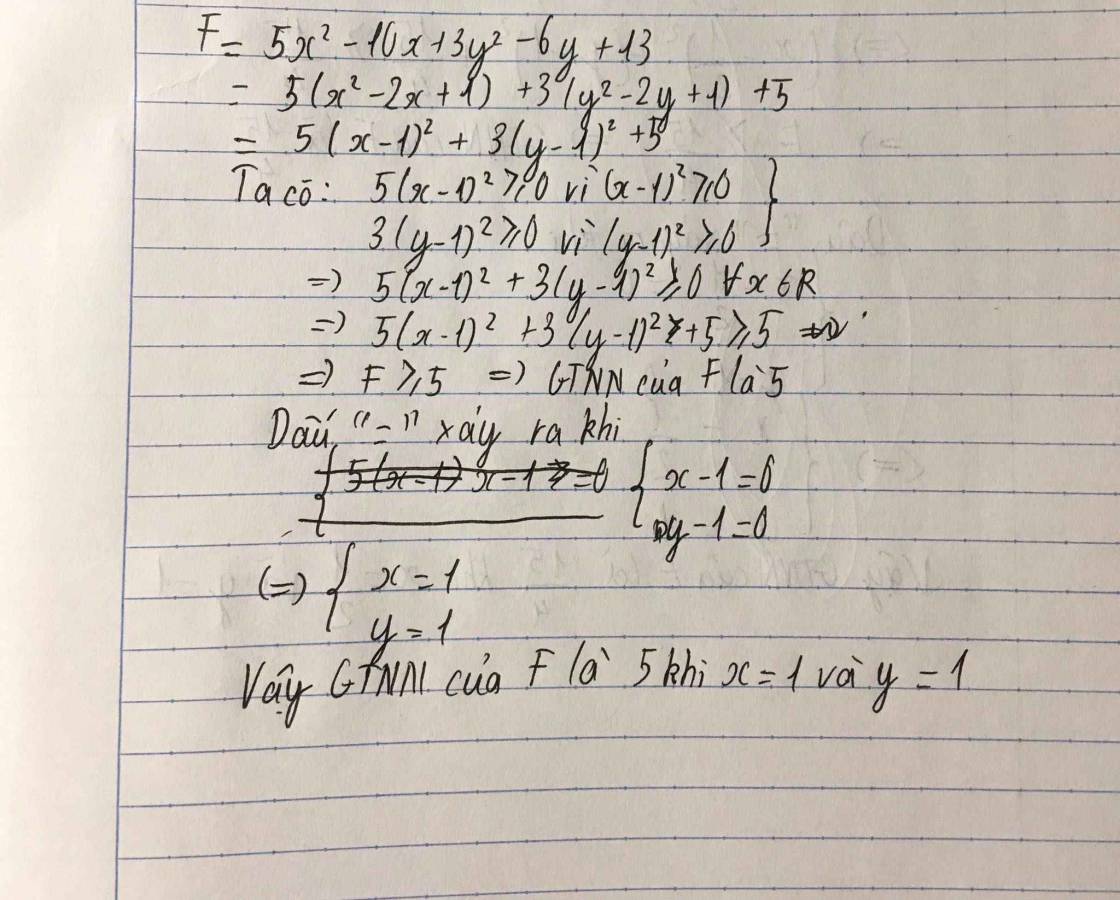
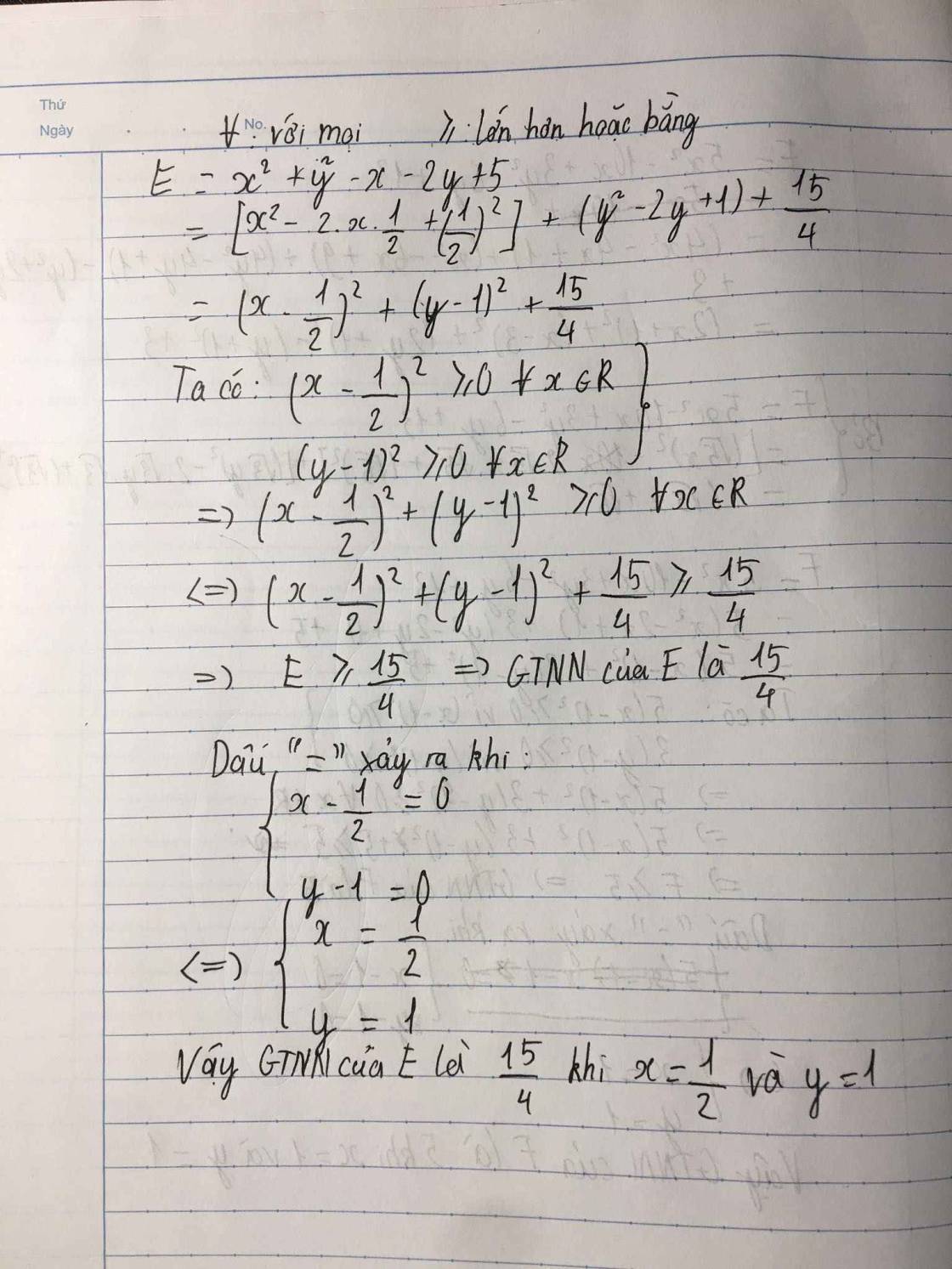
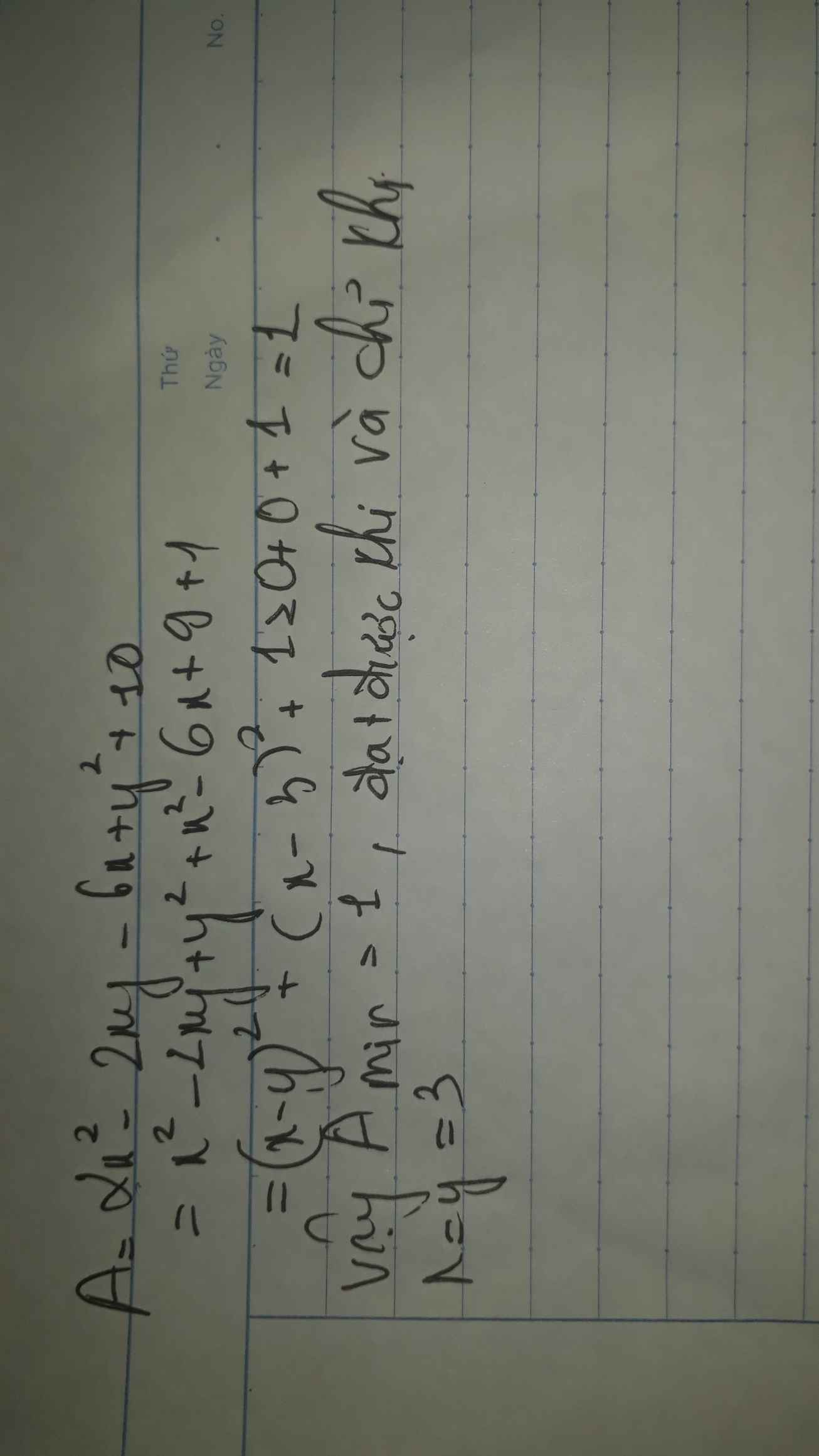
bạn ơi những câu như thế này bạn không nên lên đây hỏi vì nếu những câu này mà bạn không biết làm thì bạn phải đi hỏi giáo viên để giáo viên kiểm tra lại trình độ học vấn của bạn
ko bt thì mới hỏi chứ bạn, nếu đã biết như bạn thì cậu đã ko hỏi Nguyễn Vũ