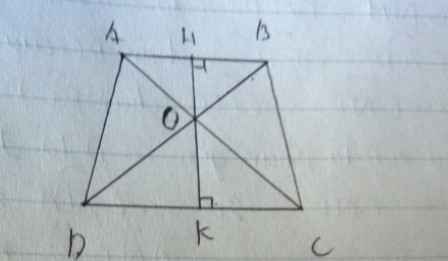
Cho hình thang ABCD. Hãy so sánh diện tích hai tam giác AOD và BOC. A B C D O ...
Đọc tiếp
Cho hình thang ABCD. Hãy so sánh diện tích hai tam giác AOD và BOC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 1 2019
Bài giải dài lắm xin lỗi bạn nha. Nếu được thì cho mình địa chỉ mail nhé. Mình gửi lời giải cho
NB
27 tháng 6 2021
\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
27 tháng 4
Vì AB//CD
nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
Ta có: \(\dfrac{S_{BOA}}{S_{BOC}}=\dfrac{OA}{OC}\)
\(\dfrac{S_{BOA}}{S_{AOD}}=\dfrac{OB}{OD}\)
mà \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
nên \(S_{BOC}=S_{AOD}\)
15 tháng 1 2016
bạn vẽ hình ra rồi nhìn vào đoạn thẳng để so sánh.
Cố lên nha!
15 tháng 1 2016
Gọi d(A;a) là khoảng cách từ điểm A đến đường thẳng a.
2S(AOB) =OB.d(A;OB) =8
2S(BOC) =OB.d(C;OB) =16
=> d(A;OB)/d(C;OB) =1/2
=> OD.d(A;OB)/[OD.d(C;OB)] =1/2
=> 2S(AOD)/(2S(COD)) =1/2
=> S(COD) =2S(AOD) =2S(BOC) =2.8 =16
=> S(ABCD) =4 +8 +8 +16 =36 (cm2)
12 tháng 1 2020
bạn ơi đề sai rồi phải không sao hai đáy trùng nhau được?