Tính giá trị biểu thức
Biết a = - 5 và b = - 6
a, a2 - 2ab + b2
b, ( a - b) 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay a = -2, b = 4 vào biểu thức ta được:
( − 2 ) 2 + 2. ( − 2 ) .4 + 4 2 − 1 = 4 + ( − 16 ) + 16 − 1 = 3
`a^2 + 2ab+b^2-1`
`= (a+b)^2-1`
`=(a+b)^2 - 1^2`
`=(a+b-1)(a+b+1)`
`= (-2+4-1)(-2+4+1)`
`= 3`

Vì |a| = 1,5 nên a = 1,5 hoặc a = -1,5
Với a = 1,5; b = -0,75. Ta có:
M = 1,5 + 2.1,5( - 0,75) – (-0,75)
= 1,5 + ( -2,25) + 0,75
= (1,5 + 0,75) + (-2,25)
= 2,25 + (-2,25) = 0
N = 1,5 : 2 -2 : ( -0,75)
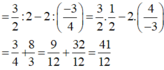
P = (-2) : (1,5)2 - (-0,75).(2/3)
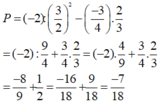
Với a = -1,5; b = -0,75 ta có:
M = - 1,5 + 2.(-1,5) ( - 0,75) – (-0,75)
= - 1,5 + ( 2,25) + 0,75
= (2,25+ 0,75) - 1,5
= 3 – 1,5 = 1,5
N = - 1,5 : 2 - 2 : ( -0,75)
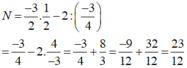
P = (-2) : (-1,5)2 — (-0,75).(2/3)
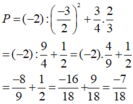

\(x^5+y^5=\left(x^2+y^2\right)\left(x^3+y^3\right)-x^2y^3-x^3y^2\)
\(=\left(x^2+y^2\right)\left(x^3+y^3\right)-\left(xy\right)^2\left(x+y\right)\)
\(=10.26-\left(-3\right)^2.2=...\)
(x+y)5=32
⇔ x5+5x4y+10x3y2+10x2y3+5xy4+y5 = 32
⇔ x5+y5 = 32-5xy(x3+y3)-10x2y2(x+y)
= 32-5.(-3).26-10.(-3)2.2
= 242

a) Rút gọn M = -6ab(-2b + a). Tính được M = 60.
b) Rút gọn M = 6xy – 7. Tính được N = -10.

a) Thay a = − 2 , b = 4 vào biểu thức ta được ( − 2 ) 2 + 2. ( − 2 ) .4 + 4 2 − 1 = 4 + ( − 16 ) + 16 − 1 = 3
b) Thay x = 4 vào biểu thức ta được 4. ( − 234 ) + ( − 4 ) .16 = ( − 4 ) .234 + ( − 4 ) .16 = ( − 4 ) . ( 234 + 16 ) = ( − 4 ) .250 = − 1000

\(\left(a+b+c\right)^2=a^2+b^2+c^2\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
\(\Leftrightarrow2\left(ab+bc+ac\right)=0\Leftrightarrow ab+bc+ac=0\Leftrightarrow bc=-ab-ac\)
\(\dfrac{a^2}{a^2+2bc}=\dfrac{a^2}{a^2+bc-ac-ab}=\dfrac{a^2}{\left(a-c\right)\left(a-b\right)}\)
CMTT: \(\left\{{}\begin{matrix}\dfrac{b^2}{b^2+2ca}=\dfrac{b^2}{\left(b-a\right)\left(b-c\right)}\\\dfrac{c^2}{c^2+2ab}=\dfrac{c^2}{\left(c-a\right)\left(c-b\right)}=\dfrac{c^2}{\left(a-c\right)\left(b-c\right)}\end{matrix}\right.\)
\(\Rightarrow A=\dfrac{a^2}{\left(a-c\right)\left(a-b\right)}+\dfrac{b^2}{\left(b-a\right)\left(b-c\right)}+\dfrac{c^2}{\left(a-c\right)\left(b-c\right)}=\dfrac{a^2\left(b-c\right)-b^2\left(a-c\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=1\)
Vì sao bước thứ 2 từ dưới lên lại có thể suy ra (a−b)(b−c)(a−c)/(a−b)(b−c)(a−c)=1?