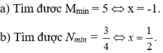Tìm giá trị nhỏ nhất của biểu thức \(|25^n-7^m-3^m|\) biết \(m,n\inℤ\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2021
Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)
\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)
Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)
Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)
Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)
a) \(P=1957\)
b) \(S=19.\)
PT
1
NN
1
17 tháng 12 2021
a) \(M=2022-\left|x-9\right|\le2022\)
\(maxM=2022\Leftrightarrow x=9\)
b) \(N=\left|x-2021\right|+2022\ge2022\)
\(minN=2022\Leftrightarrow x=2021\)
DN
16 tháng 10 2018
\(a,P=2x^2+10x+25=2\left(x^2+5x+\dfrac{25}{2}\right)\)
\(=2\left[x^2+2.x.\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2-\dfrac{25}{4}+\dfrac{25}{2}\right]\)
\(=2\left[\left(x+\dfrac{5}{2}\right)^2+\dfrac{25}{4}\right]\)
\(=2\left(x+\dfrac{5}{2}\right)^2+\dfrac{25}{2}\ge\dfrac{25}{2}>0\) với mọi x (dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{5}{2}\))
Vậy \(P_{min}=\dfrac{25}{2}\) tại \(x=-\dfrac{5}{2}\)
\(b,Q=5x-x^2=-\left(x^2-5x\right)\)
\(=-\left[x^2-2.x.\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2-\dfrac{25}{4}\right]\)
\(=-\left[\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\right]\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}< 0\) với mọi x (dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{5}{2}\))
Vậy \(Q_{max}=\dfrac{25}{4}\) tại \(x=\dfrac{5}{2}\)
C, đề sai
9 tháng 2 2021
a) Ta có: \(\left(2x-4\right)^4\ge0\forall x\)
\(\Leftrightarrow\left(2x-4\right)^4+5\ge5\forall x\)
Dấu '=' xảy ra khi 2x-4=0
\(\Leftrightarrow2x=4\)
hay x=2
Vậy: Giá trị nhỏ nhất của biểu thức \(M=\left(2x-4\right)^2+5\) là 5 khi x=2
b) Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\Leftrightarrow-\left|x+2\right|\le0\forall x\)
\(\Leftrightarrow\left|x+2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x+2=0
hay x=-2
Vậy: Giá trị lớn nhất của biểu thức \(N=10-\left|x+2\right|\) là 10 khi x=-2
NT
1