So sánh số : 202303 và 303202
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
4 tháng 10 2023
202³⁰³ = (202³)¹⁰¹ = 8242408¹⁰¹
303²⁰² = (303²)¹⁰¹ = 91809¹⁰¹
Do 8242408 > 91809 nên 8282408¹⁰¹ > 91809¹⁰¹
Vậy 202³⁰³ > 303²⁰²
19 tháng 8 2023
a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)
29 tháng 6 2021
a, Ta có : \(8>7\)
\(\Rightarrow2^{13}.8=2^{16}>2^{13}.7\)
b, Ta có : \(199^{20}< 200^{20}=2^{60}.5^{40}\)
Mà \(2003^{15}>2000^{15}=2^{60}.2^{45}\)
Thấy : \(45>40\)
\(\Rightarrow2000^{15}>200^{20}\)
\(\Rightarrow2003^{15}>199^{20}\)
c, Ta có : \(\left\{{}\begin{matrix}202^{303}=\left(2.101\right)^{3.101}=\left(8.101^3\right)^{101}\\303^{202}=\left(3.101\right)^{2.101}=\left(9.101^2\right)^{101}\end{matrix}\right.\)
Mà \(8.101^3>9.101^2\)
\(\Rightarrow202^{303}>303^{202}\)
29 tháng 6 2021
a) Ta có: \(2^{16}=2^{13}\cdot8\)
mà \(7< 8\)
nên \(7\cdot2^{13}< 2^{16}\)
b) \(199^{20}=1568239201^5\)
\(2003^{15}=8036054027^5\)
mà \(1568239201< 8036054027\)
nên \(199^{20}< 2003^{15}\)
c) Ta có: \(202^{303}=\left(202^3\right)^{101}\)
\(303^{202}=\left(303^2\right)^{101}\)
mà \(202^3>303^2\)
nên \(202^{303}>303^{202}\)
24 tháng 10 2021
a: \(2^{300}=8^{100}\)
\(3^{200}=9^{100}\)
mà 8<9
nên \(2^{300}< 3^{200}\)
b: \(3^{500}=243^{100}\)
\(7^{300}=343^{100}\)
mà 243<243
nên \(3^{500}< 7^{300}\)
2 tháng 7 2021
a) \(243^5=\left(3^5\right)^5=3^{25}\)
\(3\cdot27^5=3\cdot\left(3^3\right)^5=3\cdot3^{15}=3^{16}\)
mà \(3^{25}>3^{16}\)
nên \(243^5>3\cdot27^5\)
b) \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
mà \(5^{20}< 5^{21}\)
nên \(625^5< 125^7\)
c) \(202^{303}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=\left(303^2\right)^{101}=91809^{101}\)
mà \(8242408^{101}>91809^{101}\)
nên \(202^{303}>303^{202}\)
21 tháng 2 2022
a) ta có: \(1-\frac{2012}{2013}=\frac{1}{2013}\)
\(1-\frac{2013}{2014}=\frac{1}{2014}\)
mà \(\frac{1}{2013}>\frac{1}{2014}\) nên \(\frac{2013}{2014}>\frac{2012}{2013}\)
CM
12 tháng 2 2019
Hướng dẫn giải:
So sánh 11 8 v à 9 7 . Quy đồng mẫu số của 11 8 v à 9 7 được 77 56 v à 72 56 .
Mà 77 56 > 72 56 . Vậy 11 8 > 9 7
VA
15 tháng 5 2021
11/8>9/7 vo\ì quy đồng mẫu số của 11/8 đc 77/56,quy đồng mẫu số của 9/7 đc 72/56 mà 77/56>72/56 nên 11/8 lớn hơn
CM
5 tháng 10 2018
Hướng dẫn giải:
So sánh 7 5 v à 8 3 . Quy đồng mẫu số của 7 5 v à 8 3 được 21 15 v à 40 15 .
Mà 21 15 < 40 15 . Vậy 7 5 < 8 3
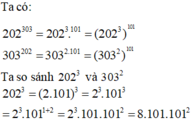
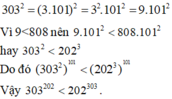
Ta co : 202303 va 303202
=> 202303=(2022)101=40804101 (1)
=>303202=(3033)101=27818127101 (2)
Tu (1) va (2) suy ra 202303<303202
lik e nhe