Cho xOy và xOm là 2 góc kề bù . Biết xOy = 2 xOm . Tính xOy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
19 tháng 3 2019
Giải
O y x z m
a) +) Tính \(\widehat{xOy}\)
Theo đề bài, ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\) (kề bù)
hay \(\widehat{xOy}+5\widehat{xOy}=180^0\)
\(\Leftrightarrow6\widehat{xOy}=180^0\)
\(\Leftrightarrow\widehat{xOy}=180^0\div6\)
\(\Leftrightarrow\widehat{xOy}=30^0\)
+) Tính \(\widehat{yOz}\)
Theo đề bài, ta có: \(\widehat{yOz}=5\widehat{xOy}\)
hay \(\widehat{yOz}=5.30^0\)
\(\Leftrightarrow\widehat{yOz}=150^0\)
b) Vì Om là tia phân giác của \(\widehat{yOz}\) nên \(\widehat{yOm}=\widehat{mOz}=\frac{\widehat{yOz}}{2}=\frac{150^0}{2}=75^0\)
Vì Om nằm giữa Oz và Oz mà \(\widehat{xOy}\) và \(\widehat{yOz}\) kề bù nên Oy nằm giữa Ox và Om.
\(\Rightarrow\widehat{xOy}+\widehat{yOm}=\widehat{xOm}\)
hay \(30^0+75^0=\widehat{xOm}\)
\(\Leftrightarrow\widehat{xOm}=105^0\)
Vậy \(\widehat{xOm}=105^0\)
9 tháng 2 2022
1: \(\widehat{yOz}=\dfrac{180^0}{4}=45^0\)
2: \(\widehat{xOt}=\dfrac{135^0}{2}=67.5^0\)
=>\(\widehat{xOm}=112.5^0\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 12 2023
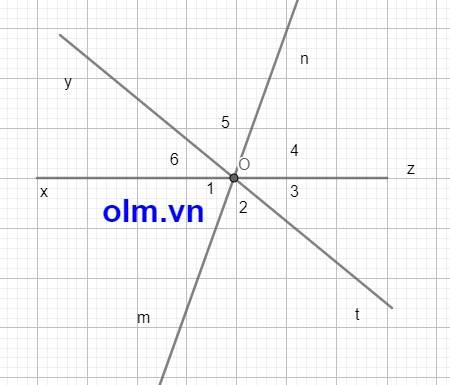
Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1)
Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng
\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh
⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)
Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 1800 (gt)
⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) = 1800
⇒ Om và On cùng thuộc một đường thẳng mn (2)
Kết hợp (1) và (2) ta có: góc zOn và góc xOm là hai góc đối đỉnh
S
25 tháng 8 2021
Bạn vẽ hình vào nhé
A) góc xOy kề bù yOz suy ra xOy+yOz=180 độ
mà xOy=60 độ suy ra yOz=120 độ
b) Om pg yOz mà yOz=120 độ suy ra Om =60 độ
mà xOy=60 độ suy ra Oy pg xOm
25 tháng 8 2021
a: Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)
\(\Leftrightarrow\widehat{yOz}=180^0-60^0\)
hay \(\widehat{yOz}=120^0\)
21 tháng 8 2019
X O Y Z M
Vì góc XOY kề bù với YOZ nên góc YOZ = 180 - 50 = 130 độ
Vì OM và tia đối của OY nên góc YOM = 180 độ
Mà góc YOZ bằng 130 độ => góc MOZ= 180 -130= 50 độ
Góc XOM = 180 - góc MOX = 180 - 50=130 độ
Vậy YOZ=XOM và XOY = MOZ
21 tháng 8 2019
O X Z Y M
Vì \(\orbr{\begin{cases}\widehat{xOy}+\widehat{yOz}=180^o\\\widehat{zOm}+\widehat{yOz}=180^o\end{cases}\Rightarrow\widehat{xOy}=\widehat{zOm}}\) ( đpcm )
Vì \(\hept{\begin{cases}\widehat{xOy}+\widehat{xOm}=180^0\\\widehat{zOm}+\widehat{zOy}=180^0\\\widehat{xOy}=\widehat{zOM}\left(cmt\right)\end{cases}\Rightarrow\widehat{xOm}=\widehat{zOy}}\) ( đpcm )
cmt là chứng minh trên nha
Study well
Vì hai góc \(\widehat{xOy}\)và \(\widehat{xOm}\)là hai góc kề bù nên ta có : \(\widehat{xOy}+\widehat{xOm}=180^0\)
Mà \(\widehat{xOy}=2\widehat{xOm}\)nên \(2\widehat{xOm}+\widehat{xOm}=180^0\)
\(\Rightarrow3\widehat{xOm}=180^0\)
\(\Rightarrow\widehat{xOm}=60^0\)
Thay xOm = 600 ta lại có : \(\widehat{xOy}=2\widehat{xOm}\)
\(\Rightarrow\widehat{xOy}=2\cdot60^0=120^0\)
Vậy : ...
Bài giải
O x y m
Vì hai góc \(xOy\) và \(xOm\) kề bù \(\Rightarrow\text{ }\widehat{xOy}+\widehat{xOm}=180^o\)
Mà \(\widehat{xOy}=2\widehat{xOm}\)
\(\Rightarrow\text{ }2\widehat{xOm}+\widehat{xOm}=180^o\)
\(3\widehat{xOm}=180^o\)
\(\Rightarrow\text{ }\widehat{xOm}=180^o\text{ : }3\)
\(\Rightarrow\text{ }\widehat{xOm}=60^o\)
\(\Rightarrow\text{ }\widehat{xOy}=60\cdot2=120^o\)