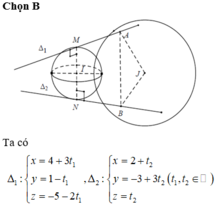
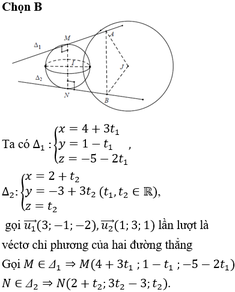
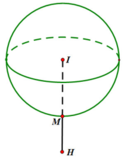
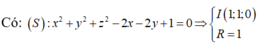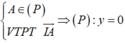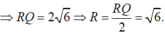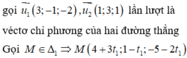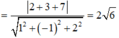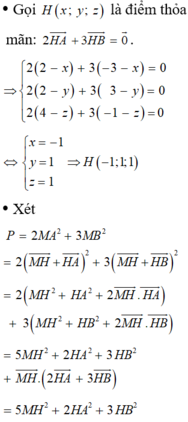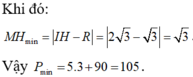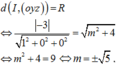Trong không gian Oxyz, cho mặt cầu (S): \(x^2 y^2 (z \sqrt(2))^2 = 3\)Có tất cả bao nhiêu điểm A(a

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

NH

Nguyễn Hoàng Sơn

25 tháng 7 2019 - olm

Trong không gian Oxyz, cho mặt cầu (S): \(x^2 + y^2 + (z+\sqrt(2))^2 = 3\)

Có tất cả bao nhiêu điểm A(a; b; c) (a, b, c là các số nguyên) thuộc mặt phẳng (Oxy) sao cho có ít nhất hai tiếp tuyến của (S) đi qua A và hai tiếp tuyến đó vuông góc với nhau?

#Toán lớp 12

0

Những câu hỏi liên quan

PT

Pham Trong Bach

26 tháng 10 2018

Trong không gian Oxyz, cho hai điểm A (1;0;0), B (0;0;2) và mặt cầu (S): x²+y²+z²-2x-2y+1=0. Hỏi có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với (S). A.3. B. 0 C. 1 ...

#Toán lớp 12

1

CM

Cao Minh Tâm

26 tháng 10 2018

Chọn C

Gọi (P) là mặt phẳng thỏa mãn bài toán.

Ta có A (1; 0; 0) ∈ (S) => nếu tồn tại (P) thì (P) tiếp xúc với (S) tại A.

Ta thấy A (0; 0 ; 2) ∈ (P) duy nhất một mặt phẳng thỏa mãn bài toán.

Ghi chú: Bài toán này thường thường thì sẽ có hai mặt phẳng thỏa mãn, nhưng với số liệu của bài này thì chỉ có một mặt phẳng thỏa mãn bài toán.

PT

Pham Trong Bach

24 tháng 1 2018

Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và △ 2 : x - 2 = y + 3 = z 1 Trong tất cả các mặt cầu tiếp xúc với cả hai đường thẳng △ 1 và △ 2 Gọi (S) là mặt cầu có bán kính nhỏ...

#Toán lớp 12

1

CM

Cao Minh Tâm

24 tháng 1 2018

Đáp án B.

PT

Pham Trong Bach

22 tháng 4 2018

Trong không gian Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + ( y + 1 ) 2 + ( z + 2 ) 2 = 4 và mặt phẳng (P): 4x-3y-m=0. Tìm tất cả các giá trị thực của tham số m để mặt phẳng (P) và mặt cầu (S) có đúng 1 điểm chung A. m=1 B. m=-1 hoặc m=-21 C. m=1 hoặc m=21 D. m=-9 hoặc...

#Toán lớp 12

1

CM

Cao Minh Tâm

22 tháng 4 2018

Đáp án C.

PT

Pham Trong Bach

17 tháng 11 2019

Trong không gian Oxyz, cho hai đường thẳng ∆ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và ∆ 2 : x - 2 1 = y + 3 3 = z 1 . Trong tất cả mặt cầu tiếp xúc với cả hai đường thẳng ∆ 1 và ∆ 2 . Gọi (S) là...

#Toán lớp 12

1

CM

Cao Minh Tâm

17 tháng 11 2019

PT

Pham Trong Bach

25 tháng 3 2018

Trong không gian Oxyz, cho hai đường thẳng Δ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và Δ 2 : x - 2 1 = y + 3 3 = z 1 . Trong tất cả mặt cầu tiếp xúc với cả hai đường thẳng Δ 1 v à Δ 2 . Gọi (S) là mặt cầu...

1

CM

Cao Minh Tâm

25 tháng 3 2018

PT

Pham Trong Bach

19 tháng 2 2017

Trong không gian Oxyz, cho hai điểm A(2;-2;4), B(-3;3;-1) và mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 3 ) 2 + ( z - 3 ) 2 = 3 . Xét điểm M thay đổi thuộc mặt cầu (S), giá trị nhỏ nhất của 2 M A → 2 + 3 M B → 2 bằng A. 103 B. 108 C. 105 D....

#Toán lớp 12

1

CM

Cao Minh Tâm

19 tháng 2 2017

Đáp án C.

PT

Pham Trong Bach

15 tháng 2 2018

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): ( x + 3 ) 2 + y 2 + ( z - 2 ) 2 = m 2 + 4 . Tìm tất cả các giá trị thực của tham số m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz). ...

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 2 2018

Chọn D

PT

Pham Trong Bach

23 tháng 5 2019

Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9 điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là A. ( P ) : x + 2 y + 3 z + 6 = 0 B. ( P ) : ...

1

CM

Cao Minh Tâm

23 tháng 5 2019

Chọn B

A

AllesKlar

15 tháng 5 2022

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left(S\right):\left(x+1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=48\) và đường thẳng \(\left(d\right):\dfrac{x+1}{1}=\dfrac{y-2}{1}=\dfrac{z-3}{\sqrt{2}}\) . Điểm \(M\left(a;b;c\right)\left(a0\right)\) nằm trên đường thẳng \(\left(d\right)\) sao cho từ \(M\) kẻ được 3 tiếp tuyến \(MA,MB,MC\) đến mặt cầu \(\left(S\right)\) thỏa...

#Toán lớp 12

0