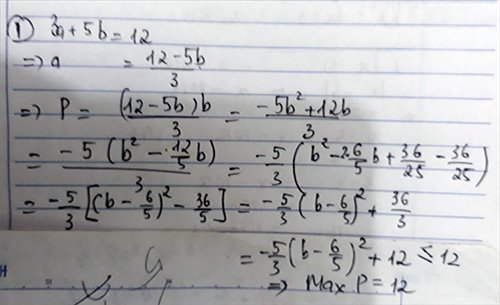\(\frac{3}{1-x}+\frac{4}{x}\)Tìm min A với 0<x<1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


https://olm.vn/hoi-dap/detail/258469425824.html . Bạn tham khảo link này
Áp dụng BĐT Cauchy cho 2 số không âm ta có :
\(A=\frac{a}{16}+\frac{1}{a}+\frac{15a}{16}\ge2\sqrt[2]{\frac{a}{16}.\frac{1}{a}}+\frac{60}{16}=\frac{17}{4}\)
Đẳng thức xảy ra khi và chỉ khi \(a=4\)
Vậy \(Min_A=\frac{17}{4}\)khi \(a=4\)

1) \(A=\frac{a}{16}+\frac{1}{a}+\frac{15a}{16}\ge2\sqrt{\frac{a}{16}.\frac{1}{a}}+\frac{15.4}{16}=\frac{17}{4}\)
Dấu "=" xảy ra <=> a = 4
Vậy min A = 17/4 tại a = 4
2) \(B=3x+\frac{16}{x^3}=x+x+x+\frac{16}{x^3}\ge4\sqrt[4]{x.x.x.\frac{16}{x^3}}=8\)
Dấu "=" xảy ra <=> x = 2
Vậy min B = 8 tại x = 2
3) 0<x<2 tìm min \(C=\frac{9x}{2-x}+\frac{2}{x}\)
Ta có: \(C=\frac{9x}{2-x}+\frac{2}{x}=\frac{9x}{2-x}+\frac{2-x}{x}+1\ge2\sqrt{\frac{9x}{2-x}.\frac{2-x}{x}}+1=7\)
Dấu "=" xảy ra <=> x = 1/2 thỏa mãn
Vậy min C = 7 đạt tại x = 1/2

Sử dụng AM - GM dạng cộng mẫu :
\(\frac{1}{x+1}+\frac{4}{y+2}+\frac{9}{z+3}\)
\(\ge\frac{\left(1+2+3\right)^2}{x+y+z+1+2+3}\)
\(=\frac{36}{x+y+z+6}\)
\(=\frac{36}{12}=3\)
Đẳng thức xảy ra tại ......
Trên kia là sai lầm thường gawpjjj ( theo mình nghĩ thế tại nhác tìm dấu bằng )
thứ 2 là wolfram alpha bảo không có minimize:


\(1,A=\frac{1}{x^2+y^2}+\frac{1}{xy}=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\)
\(\ge\frac{4}{\left(x+y^2\right)}+\frac{1}{\frac{\left(x+y\right)^2}{2}}\ge\frac{4}{1}+\frac{2}{1}=6\)
Dấu "=" <=> x= y = 1/2
\(2,A=\frac{x^2+y^2}{xy}=\frac{x}{y}+\frac{y}{x}=\left(\frac{x}{9y}+\frac{y}{x}\right)+\frac{8x}{9y}\ge2\sqrt{\frac{x}{9y}.\frac{y}{x}}+\frac{8.3y}{9y}\)
\(=2\sqrt{\frac{1}{9}}+\frac{8.3}{9}=\frac{10}{3}\)
Dấu "=" <=> x = 3y

2. Xem tại đây
1. \(P=\frac{1}{\sqrt{x.1}}+\frac{1}{\sqrt{y.1}}+\frac{1}{\sqrt{z.1}}\)
\(\ge\frac{1}{\frac{x+1}{2}}+\frac{1}{\frac{y+1}{2}}+\frac{1}{\frac{z+1}{2}}\)
\(=\frac{2}{x+1}+\frac{2}{y+1}+\frac{2}{z+1}\ge\frac{2.\left(1+1+1\right)^2}{x+y+z+3}=\frac{18}{3+3}=3\)
Đẳng thức xảy ra \(\Leftrightarrow x=y=z=1\)
1 ) có cách theo cosi đó
áp dụng cosi cho 3 số dương ta có \(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{x}}+x\ge3\sqrt[3]{\frac{1}{\sqrt{x}}\times\frac{1}{\sqrt{x}}\times x}=3\sqrt[3]{1}=3\)(1)
\(\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{y}}+y\ge3\)(2)
\(\frac{1}{\sqrt{z}}+\frac{1}{\sqrt{z}}+z\ge3\)(3)
cộng các vế của (1),(2),(3), đc \(2\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}\right)+\left(x+y+z\right)\ge9\Rightarrow2P+3\ge9\Rightarrow P\ge3\)
minP=3 khi x=y=z=1