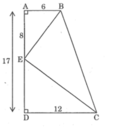
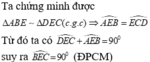Hình thangABCD, AB=6cm, CD=12cm, AD=10cm, E thuộc AD sao cho AE=8cm .Chứng minh BE vuông góc với EC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét △ ABE và △ DEC, ta có:
∠ A = ∠ D = 90 0 (1)
Mà :
Suy ra: 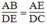 (2)
(2)
Từ (1) và (2) suy ra : △ ABE đồng dạng △ DEC (c.g.c)
Suy ra: ∠ ABE = ∠ DEC
Trong △ ABE ta có: ∠ A = 90 0 ⇒ ∠ (AEB) + ∠ (ABE) = 90 0
Suy ra: ∠ (AEB) + ∠ (DEC) = 90 0
Lại có: ∠ (AEB) + ∠ (BEC) + ∠ (DEC) = 180 0 (kề bù)
Vậy : ∠ (BEC) = 180 0 - ( ∠ (AEB) + ∠ (DEC)) = 180 0 - 90 0 = 90 0

a)Xét hình bình hành ABED có:
AB=DE
AB//DE(doAB//DC)
=>tứ giác ABED là hình bình hàXetnh vì có 2 cạnh đối // và = nhau(dấu hiệu nhận biết thứ 3)
b)Có AB//DE=>gócBAE=góc AED(2 góc so le trong )
Xét tam giác ANI và tam giác EMI có:
AI=IE(là trung điểm AI)
góc BAE=gócAED(cmt)
góc AIN=gócEIM(2 góc đối đỉnh)
=>tam giác ANI=tam giác EIM(g.c.g)
=>AN=ME(2 cạnh tương ứng)
có AB=DE
AN=ME
=>AB-AN=DE-ME
=>NB=DM
mà DM=MC(do M là trung điểm DC)
=>NB=MC
Lại có NB//MC (do AB//DC)
Xét tứ giác NBMC có :
NB=MC(cmt)
NB//MC(cmt)
=>tứ giác NBMC là hình bình hành vì có 2 cạnh đối //và= nhau(dhnb thứ 3)
=>NM=BC
c)

Bạn nên ktra lại con số 15cm
a/ Áp dụng định lí Pythagoras cho t/g ABC vuông tại A có
\(AB^2+AC^2=BC^2\)
=> \(AC=\sqrt{161}\) (cm)
b/ t/g ABH vuông tại H và t/g EBH vuông tại H có
AB = EB
BH : chung
=> t/g ABH=t/g EBH (ch-cgv)
=> HA = HE (2 cạnh t/ứ)
c/ Có \(\widehat{BAH}=\widehat{BEH}\) (do t/g ABH = t/g EBH)
=> \(180^o-\widehat{BAH}=180^o-\widehat{BEH}\)
=> \(\widehat{EAD}=\widehat{AEC}\)
=> t/g AEC = t/g EAD
=> AC = DE
d/
AB = BEAD = EC
=> AB + AD = BE + EC
=> BD = BC=> t/g BCD cân tại B
Có t/g ABH = t/g EBH
=> \(\widehat{ABH}=\widehat{EBH}\)
=> BH là pg góc ABEHay BH là pg góc DBCXét t/g BDC có BH là đường pg
=> BH đồng thời là đường cao
=> BH ⊥ DC

a: Xét ΔABE vuông tại E và ΔACD vuông tại D có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACD
b: \(CD=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: Ta có: ΔABE=ΔACD
nên AE=AD
d: Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
DC=BE
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔBIC cân tại I