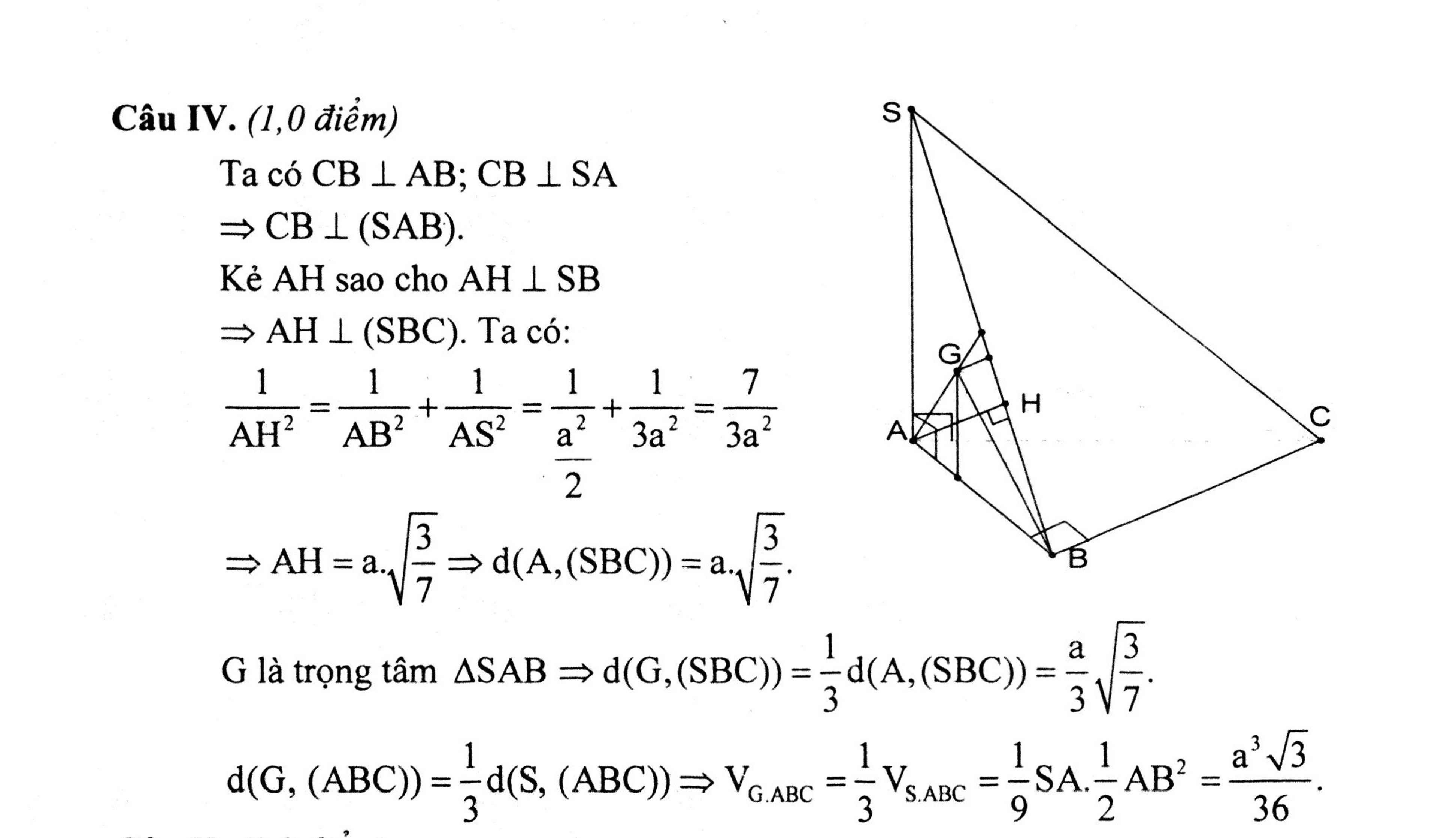
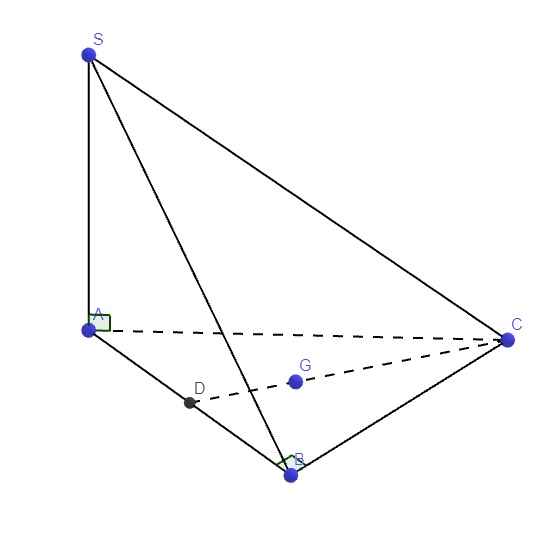
Cho tam giác ABC vuông cân tại A, có trọng tâm G.
Gọi E; H lần lượt là trung điểm của các cạnh AB; BC.
D là điểm đối xứng của H qua A
I là giao điểm của đường thẳng AB và đường thẳng CD
Gọi K là trung điểm của BI
a.CMR: Tam giác AKH = tam giác AID
b. CMR: tứ giác AGCI nội tiếp
c. CMR: IG.AB= BK.DE