Cho hình chữ nhật ABCD có AB=8cm, AD=4cm. Gọi M là trung diểm cạnh CD, N là một điểm trên đường chéo AC sao cho NC=3NA. Tính độ dài MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ΔADC vuông tại D
=>\(AC^2=AD^2+DC^2\)
=>\(AC^2=8^2+6^2=100\)
=>AC=10(cm)
ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>M là trung điểm chung của AC và BD và AC=BD
=>MD=MB=MA=MC=AC/2=5(cm)
Xét ΔDME vuông tại M và ΔDCB vuông tại C có
\(\widehat{MDE}\) chung
Do đó: ΔDME đồng dạng với ΔDCB
=>\(\dfrac{ME}{CB}=\dfrac{DM}{DC}\)
=>\(\dfrac{ME}{6}=\dfrac{5}{8}\)
=>\(ME=3,75\left(cm\right)\)

a: \(AC=\sqrt{15^2+8^2}=17\left(cm\right)\)
OD=AC/2=8,5cm
b: Xét tứ giác ADPC có
M là trung điểm chung của AP và DC
nên ADPC là hình bình hành
=>DP=AC=2OC
c: Xét tứ giác OBEC có
N là trung điểm chung của OE và bC
OB=OC
Do dó: OBEC là hình thoi

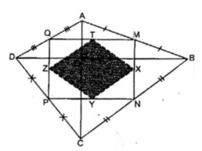
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.
Từ NC = 3 NA => NC = 3/4 CA
Kẻ NH _|_CD
=> NH // AD
Theo Ta-let có
\(\frac{NH}{AD}=\frac{CN}{CA}=\frac{\frac{3}{4}CA}{CA}=\frac{3}{4}\)
\(\Rightarrow NH=\frac{3AD}{4}=\frac{3.4}{4}=3\)
Theo Pytago có \(AD^2+DC^2=AC^2\)
\(\Leftrightarrow4^2+8^2=AC^2\)
\(\Leftrightarrow AC^2=80\)
\(\Leftrightarrow AC=4\sqrt{5}\)
\(\Rightarrow NC=\frac{3}{4}AC=\frac{3}{4}.4\sqrt{5}=3\sqrt{5}\)
Áp dụng định lí Pytago \(NH^2+HC^2=NC^2\)
\(\Leftrightarrow3^2+HC^2=45\)
\(\Leftrightarrow HC^2=36\)
\(\Leftrightarrow HC=6\)
CÓ \(MC=\frac{CD}{2}=\frac{8}{2}=4\)
\(\Rightarrow HM=HC-CM=6-4=2\)
Áp dụng Pytago
\(HN^2+HM^2=NM^2\)
\(\Leftrightarrow3^2+2^2=NM^2\)
\(\Leftrightarrow MN^2=13\)
\(\Leftrightarrow MN=\sqrt{13}\)