Cho tam giác ABC có 3 góc nhọn và đường cao BD, CE. Vẽ BF vuông góc với ED, CK vuông góc với ED (F, D thuộc ED). Chứng minh EF=DK
Help me<3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2018
Lấy trung điểm M của cạnh BC. Gọi H là hình chiếu của M lên DE.
Xét \(\Delta\)BEC: ^BEC = 900; M là trung điểm BC => EM = 1/2.BC
Xét \(\Delta\)BDC: ^BDC = 900; M là trung điểm BC => DM = 1/2.BC
=> EM = DM => \(\Delta\)EMD cân tại M . Do MH là đường cao \(\Delta\)EMD
=> MH cũng là đường trung tuyến => H là trung điểm DE => HD = HE (1)
Xét tứ giác BFKC: BF // CK (Cúng vuông DE) => Tứ giác BFKC là hình thang (vuông)
Ta có: BF; CK; MH cùng vuông DE => MH // BF // CK
Xét hình thang BFKC: M là trung điểm BC; MH // BF // CK; H thuộc FK
=> H là trung điểm FK => HF = HK (2)
Từ (1) & (2) => HF - HE = HK - HD => EF = DK (đpcm).
HN
16 tháng 3
AH cắt đường tròn tâm O tại M . Tam giác abd có dk là đường cao nên bk.ba=bd.bd mà bk.ba = bf.bi nên bd.bd =bf.bi
Nên bf/bd=bd/bi và góc ibd chung
Nên tam giác bfd đồng dạng tam giác bdi
Nên góc bdi = góc bid mà bdi=ecb=bcm
mà góc bia= góc bca
Cộng lại được aid=dcm
Aicm nội tiếp nên aim = dcm . Từ đó suy ra aid=aim
Nên i,d,m thẳng hàng nên ah và id cắt nhau tại điểm thuộc đường trón tâm o
9 tháng 8 2015
AM giao I
tam giac EBC vuong => EI =IC => goc CEI = ECI
tam giac TEM dong dang tam giac TAE => TEM = TAE
IEC = TEM doi dinh
=> TAE=ICE
tt => IME = IBE => AEM dong dang CEB (g-g)
=> ty le thuc
=> EMB dong dang EAC
=> BME=CAE
tam giac EMB vuong => EF = FM => FME =FEM
FEM = CEH (dd)
=> EAC=HEC. => EH vuong goc vs AE
tt => DH vuong goc vs AE
=> H la truc tam cua AED
=> AH vuong goc ED
công minh nghĩ cả buổi tối. tích cho cái nhé
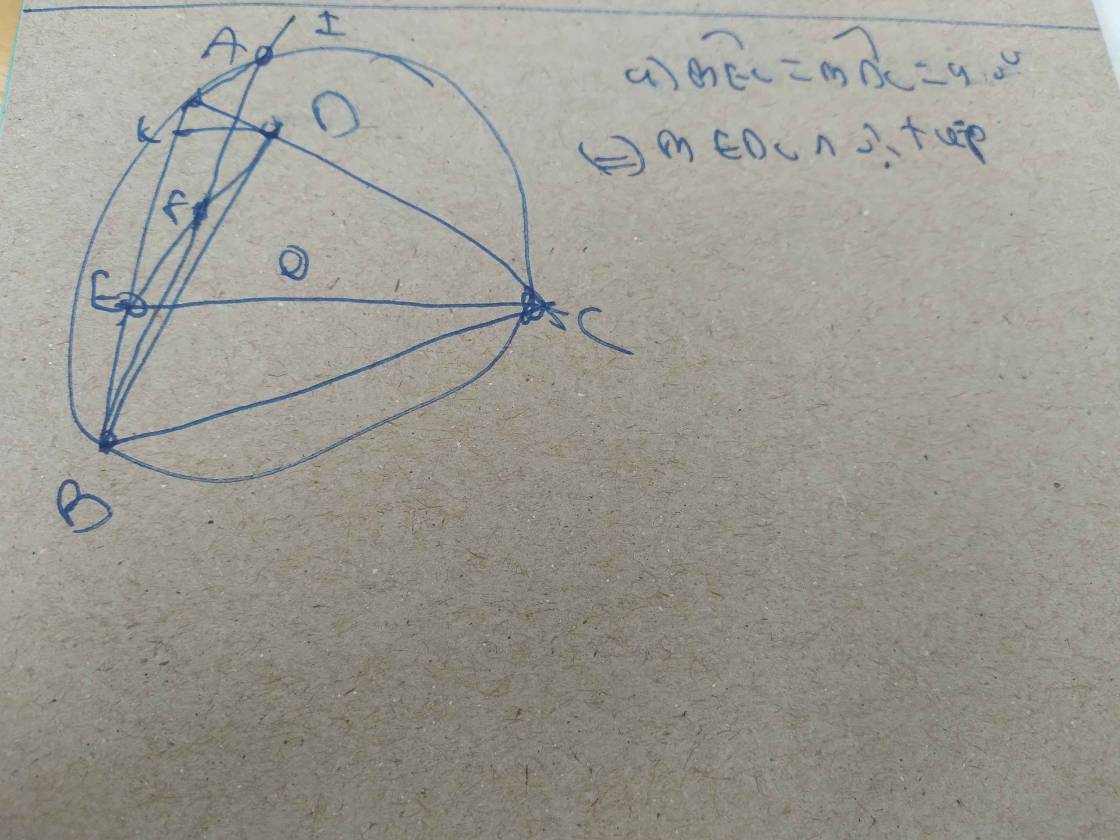
Lấy trung điểm M của cạnh BC. Gọi H là hình chiếu của M lên DE.
Xét \(\Delta\)BEC:\( \widehat{BEC}\) = 900; M là trung điểm BC => \(EM = \dfrac{1}{2}.BC\)
Xét \(\Delta\)BDC: \( \widehat{BDC}\) = 900; M là trung điểm BC => \(DM = \dfrac{1}{2}.BC\)
=> EM = DM => \(\Delta\)EMD cân tại M . Do MH là đường cao \(\Delta\)EMD
=> MH cũng là đường trung tuyến => H là trung điểm DE => HD = HE (1)
Xét tứ giác BFKC: BF // CK (Cúng vuông DE) => Tứ giác BFKC là hình thang (vuông)
Ta có: BF; CK; MH cùng vuông DE => MH // BF // CK
Xét hình thang BFKC: M là trung điểm BC; MH // BF // CK; H thuộc FK
=> H là trung điểm FK => HF = HK (2)
Từ (1) và (2) => HF - HE = HK - HD => EF = DK (đpcm).