Cho tam giác ABC, M là trung điểm của BC.Trên tia đối của MA lấy E sao cho ME = MA. Vé phân giác Ad của BAC .Qua M kẻ đt song song với AD cắt AC, AB tại F và G.CM: BG = CF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

4 tháng 2 2020
a)
Xét ΔABD và ΔAED có:
AB=AE (giả thiết)
Góc BAD= góc EAD (do AD là phân giác góc A)
AD chung
⇒⇒ ΔABD=ΔAED (c-g-c)
b) Ta có ΔABD=ΔAED
⇒⇒ BD=DE và góc ABD= góc AED
⇒⇒ Góc FBD= góc CED (hai góc kề bù với hai góc bằng nhau)
Xét ΔDBF và ΔDEC có:
BD=DE
Góc DBF= góc DEC
Góc BDF= góc EDC ( đối đỉnh )
⇒⇒ ΔDBF=ΔDEC (g-c-g)

LS
30 tháng 11 2015
Xét tam giác AMC và tam giác DMB có:
AM =MD (gt )
BM =MC (gt )
goc MAC=goc MDB(so le trong)
=>Tam giac AMC=tam giac DMB(c.g.c)
Vì góc MAD và góc MDB là hai góc so le trong tạo bởi đường thẳng AD cắt AC và BD
=>AC //BD

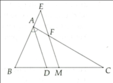

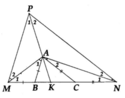
Trên tia đối của tia MG lấy điểm E sao cho MG=ME (Trên đề điểm E ko có tác dụng nên t lấy điểm E khác cho có tác dụng:V)
Ta có:
\(\Delta BGM=\Delta CEM\left(c.g.c\right)\)
\(\Rightarrow BG=CE;\widehat{BGM}=\widehat{MEC}\left(1\right)\)
Ta có:
\(\widehat{MFC}=\widehat{MAC}+\widehat{AMC}=\widehat{MAC}+\widehat{DAM}=\widehat{DAC}=\widehat{BAD}=\widehat{AGM}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\widehat{MFC}=\widehat{MEC}\Rightarrow\Delta FEC\) cân tại C
\(\Rightarrow CF=CE\)
Mà \(CE=BG\Rightarrow CF=BG\left(đpcm\right)\)
Sửa dòng thứ 6;\(\widehat{MAC}+\widehat{AMF}\) nha mọi người,mik làm hơi tắt một tí;ai ko hiểu thì cứ ib vs mik nhoa!Thanks tth_new đã nhắc