Từ một điểm A bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB và AC với (O) (B, C là các tiếp điểm). Gọi M là điểm bất kỳ nằm trên đường đi qua trung điểm Q và N của AB và AC. Từ M kẻ tiếp tuyến MK với (O) (K là tiếp điểm). Chứng minh rằng: MK=MA.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

1 tháng 10 2021
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

HB
25 tháng 4 2017
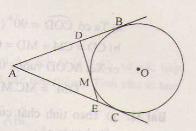
Chứng minh AB=AC; DB=DM và EC=EM.
Chu vi ΔADE bằng
= AD + DM + ME + AE
= AD + DB + EC + AE
= AB + AC
= 2AB.
KD
25 tháng 4 2017
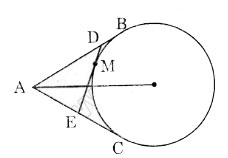
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB

CM
21 tháng 7 2017
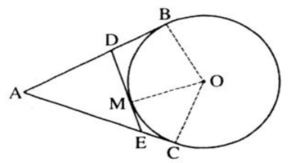
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)