GIÚP MÌNH VỚIIIIIIIII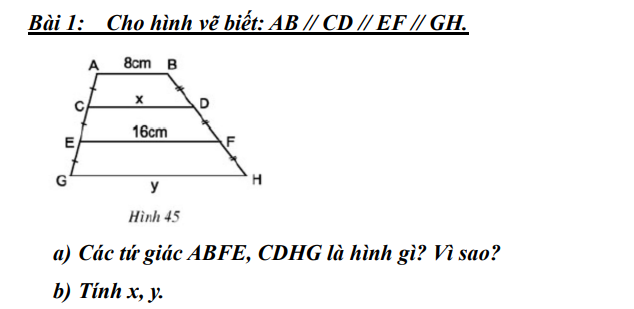
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
9 tháng 8 2021
Ta thấy rằng 2|y+1| luôn luôn lớn hơn 0
Nên suy ra được là : |x-3|+2(y+1)=6
<=>|x-3|+2y=4
<=>|x-3|=4-2y
Có hai trường hợp
1, x-3=4-2y
<=>x-7-2y=0
<=>x-2y=7
2, 3-x=4-2y
<=>x-2y=-1
Đến đây ta thấy hai kết quả khác hoàn toàn nên ko thảo mãn x và y
TA
0
PD
1
12 tháng 10 2021
\(a,\left(x-3\right)^{x+2}=\left(x-3\right)^{x+12}\\ \Leftrightarrow\left(x-3\right)^{x+2}\left[1-\left(x-3\right)^{10}\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\\ b,\left|x+2\right|=\dfrac{1}{2}-2x\Leftrightarrow\left[{}\begin{matrix}x+2=\dfrac{1}{2}-2x\left(x\ge-2\right)\\x+2=2x-\dfrac{1}{2}\left(x< -2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=-\dfrac{3}{2}\left(x\ge-2\right)\\x=\dfrac{5}{2}\left(x< -2\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\left(tm\right)\\x=\dfrac{5}{2}\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow x=-\dfrac{1}{2}\)
MMÌnh đag cần giải chi tiết 4 phần . Mình đag cần rất gấp. Mn giúp mình vớiiiiiiiii
NM
Nguyễn Minh Quang
Giáo viên
10 tháng 8 2021
ta có : \(\left(x-2\right)\left(5-x\right)\le\left(\frac{x-2+5-x}{2}\right)^2=\frac{9}{4}\)
mà vế trái \(\left|y-1\right|+1\ge1\Rightarrow\orbr{\begin{cases}\left(x-2\right)\left(5-x\right)=2\\\left(x-2\right)\left(5-x\right)=1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2-7x+12=0\\x^2-7x+11=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
khi đó \(\left|y-1\right|+1=2\Leftrightarrow\left|y-1\right|=1\Leftrightarrow\orbr{\begin{cases}y-1=1\\y-1=-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}y=2\\y=0\end{cases}}\)
Vậy ta có x bằng 3 hoặc 4 và y bằng 0 hoặc 2
các câu khác hoàn toàn tương tự nhé
10 tháng 8 2021
cho mình hỏi là ở chỗ ta có thì \(\frac{9}{4}\)là ở đâu ak
11 tháng 8 2021
\(D=\left|x-2\right|+\left|3y+9\right|+13\ge13\)
Dấu ''='' xảy ra khi x = 2 ; y = -3
Vậy GTNN của D bằng 13 tại x = 2 ; y = -3
11 tháng 8 2021
D = 13
x = 2
y = 3
nha mình phải nghĩ lâu lắm đó
xong ko biết ra hỏi anh họ :(((
14 tháng 8 2021
\(D=\left|x+3\right|+\left|x-2\right|+7=\left|x+3\right|+\left|2-x\right|+7\ge\left|x+3+2-x\right|+7=12\)
Dấu ''='' xảy ra khi \(\left(x+3\right)\left(2-x\right)\ge0\Leftrightarrow-3\le x\le2\)
Vậy GTNN của D bằng 12 tại -3 =< x =< 2
11 tháng 8 2021
Ta có: \(\left|x-5\right|\ge0\forall x\)
\(\Leftrightarrow\left|x-5\right|+12\ge12\)
\(\Leftrightarrow\frac{14}{\left|x-5\right|+12}\le\frac{7}{6}\)
\(\Leftrightarrow B\le3+\frac{7}{6}=\frac{25}{6}\)
Vậy \(MaxB=\frac{25}{6}\Leftrightarrow x=5\)
11 tháng 8 2021
Ta có : \(\left|x-5\right|+12\ge12\)
\(\Rightarrow\frac{14}{\left|x-5\right|+12}\le\frac{14}{12}=\frac{7}{6}\)
\(\Rightarrow B=3+\frac{14}{\left|x-5\right|+12}\le3+\frac{7}{6}=\frac{25}{6}\)
Dấu ''='' xảy ra khi x = 5
Vậy GTLN của B bằng 25/6 tại x = 5
a)+ Xét tứ giác ABFE có:
AB//FE (gt)
\(\Rightarrow\) Tứ giác ABFE là hình thang (định nghĩa hình thang)
+ Xét tứ giác CDHG có:
CD//HG (gt)
\(\Rightarrow\)Tứ giác CDHG là hình thang (định nghĩa hình thang)
b) Xét hình thang ABEF có:
C là trung điểm của AE
D là trung điểm của BF
\(\Rightarrow\)CD là đường trung bình của hình thang ABEF (định nghĩa đường trung bình của hình thang)
\(\Rightarrow\)CD=\(\dfrac{AB+EF}{2}\) (tính chất đường trung bình của hình thang)
hay CD=\(\dfrac{8+16}{2}\) = 12 (cm)
\(\Rightarrow\) x=12
+Xét hình thang CDHG có:
E là trung điểm của CG
F là trung điểm của DH
\(\Rightarrow\)EF là đường trung bình của hình thang CDHG (định nghĩa đường trung bình của hình thang)
\(\Rightarrow\)\(EF=\dfrac{CD+GH}{2}\) (tính chất đường trung bình của hình thang)
hay 16=\(\dfrac{12+GH}{2}\)
GH= 20 (cm)
\(\Rightarrow y=20\)