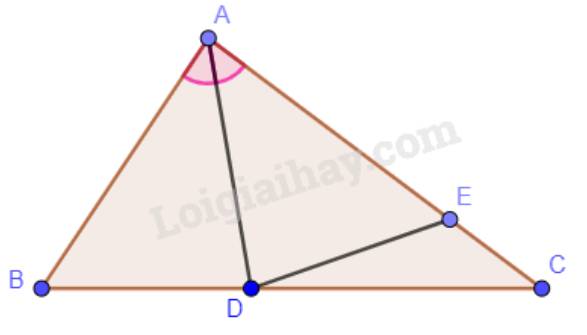
Cho \(\bigtriangleup\)ABC có \(\widehat{ABC}\) = \(\widehat{ACB}\) và có đường phân giác AD.
1) \(\widehat{ADB}\) và \(\widehat{ADC}\) là góc ngoài của những tam giác nào? Chứng minh \(\widehat{ADB} = \widehat{ADC}\)
2) So sánh \(\bigtriangleup\)ABD và \(\bigtriangleup\)ADC

1) \(\widehat{ADB}\) là góc ngoài của t/giác ABC => \(\widehat{ADB}=\widehat{C}+\widehat{DAC}\)
\(\widehat{ADC}\)là góc ngoài của t/giác AD => \(\widehat{ADC}=B+\widehat{DAB}\)
Mà \(\widehat{B}=\widehat{C}\)(gt); \(\widehat{DAB}=\widehat{DAC}\) (gt)
=> \(\widehat{DAB}=\widehat{DAC}\)
2) Xét t/giác ABD và t/giác ADC
có: \(\widehat{BAD}=\widehat{CAD}\) (gt)
AD : chung
\(\widehat{ADB}=\widehat{ADC}\)(cmt)
=> t/giác ABD = t/giác ADC (g.c.g)