Cho 3 đường thẳng aa' ; bb' ; cc' cắt nhau tại I. Tính số cặp góc đối đỉnh trên hình vẽ không tính góc bẹt ( 2 cách)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

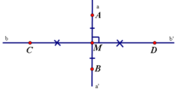
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.


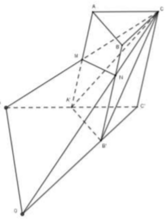
Sử dụng công thức tính thể tích khối chóp V = 1 3 h . S với h là chiều cao hình chóp và S là diện tích đáy.
Công thức tính thể tích lăng trụ V = h.S với h là chiều cao hìnhlăng trụ và S là diện tích đáy.
Cách giải:

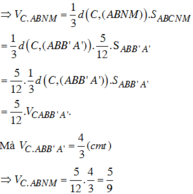
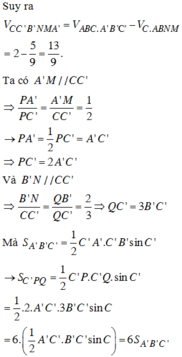

1: Xét ΔBDA có
O là trung điẻm của AB
OI//BD
=>I là trung điểm của AD
ΔOAD cân tại O
mà OI là trung tuyến
nên OI vuông góc AD và OI là phân giác của góc AOD
2: Xét ΔOAC và ΔODC có
OA=OD
góc AOC=góc DOC
OC chung
Do đó: ΔOAC=ΔODC
=>góc ODC=90 độ
=>CD là tiếp tuyến của (O)