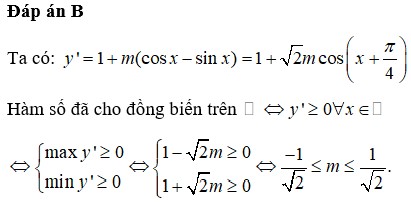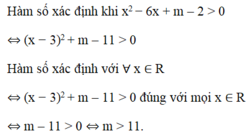\(y=\frac{Cosx}{\sqrt{Sin^6x+cos^6x+msinxcosx}}\) . Tìm tham số m để hàm số xđ trên R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm xác định trên R khi với mọi x ta có:
\(sin^6x+cos^6x+m.sinx.cosx>0\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x+\dfrac{m}{2}sin2x>0\)
\(\Leftrightarrow3sin^22x-2m.sin2x-4< 0\)
Đặt \(sin2x=t\in\left[-1;1\right]\Rightarrow3t^2-2mt-4< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}3.f\left(-1\right)< 0\\3.f\left(1\right)< 0\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2m-1< 0\\-2m-1< 0\end{matrix}\right.\)
\(\Rightarrow-\dfrac{1}{2}< m< \dfrac{1}{2}\)

1/ Để hàm số y = √cos^2(x) + cos(x) - 2m + 1 xác định trên R, ta cần điều kiện để biểu thức trong căn dương: cos^2(x) + cos(x ) - 2m + 1 > 0 Để giải phương trình này, ta sử dụng một số phép biến đổi: cos^2(x) + cos(x) - 2m + 1 = (cos(x) + 2)(cos(x) - m + 1) Điều kiện để biểu thức trên dương là: cos(x) + 2 > 0 và cos(x) - m + 1 > 0 Với cos(x) + 2 > 0, ta có -2 < cos( x) < 0 Với cos(x) - m + 1 > 0, ta có m - 1 < cos(x) < 1 Tổng Hàm, để hàm số y = √cos^2(x) + cos(x) - 2m + 1 xác định trên R, tham số m phải đáp ứng điều kiện -2 < cos(x) < 0 và m - 1 < cos(x) < 1. 2/ Để hàm số y = √cos^2(x) - 2cos(x) + m xác định trên R, ta cần điều kiện để biểu thức trong căn dương: cos^2(x) - 2cos(x) + m > 0 Đây là một phương trình bậc hai theo cos(x). Để giải phương trình này, ta sử dụng công thức delta: Δ = b^2 - 4ac Ở đây, a = 1, b = -2, c = m. Ta có: Δ = (-2)^2 - 4(1)(m) = 4 - 4m = 4(1 - m) Để phương trình có nghiệm thì Δ > 0. Tức là 1 - m > 0 hay m < 1. Tổng quát, để hàm số y = √cos^2(x) - 2cos(x) + m xác định trên R, tham số m phải đáp ứng m < 1. 3/ Để hàm số y = √sin^ 4 (x) + cos^4(x) - sin^2(x) - m xác định trên R, ta cần điều kiện để biểu thức trong căn dương: sin^4(x) + cos^4(x) - sin ^2(x) - m > 0 Đây cũng là một phương trình bậc hai theo sin(x). Ta sử dụng công thức delta as on, with a = 1, b = -1, c = -m. Δ = (-1)^2 - 4(1)(-m) = 1 + 4m = 4m + 1 Để phương trình có nghiệm thì Δ > 0. Tức là m > -1/4. Tổng quát, để hàm số y = √sin^4(x) + cos^4(x) - sin^2(x) - m xác định trên R, tham số m phải thỏa mãn m > -1/4.

Ủa sao xài hoành độ đỉnh ở đây được nhỉ, phải xài nghiệm (đúng hơn là lợi dụng quy tắc dấu tam thức bậc 2 "trong khác - ngoài cùng")
Đây, ví dụ 1 trường hợp cho em (bài này ở trên đã đưa dấu a>0 theo thói quen). 2 đường màu đỏ là khoảng \(\left(-1;\dfrac{1}{2}\right)\), rõ ràng đỉnh parabol nằm trong khoảng đó nhưng trên khoảng \(\left(-1;\dfrac{1}{2}\right)\) hàm vẫn có 1 đoạn nhận giá trị dương (tương ứng với đoạn BC)
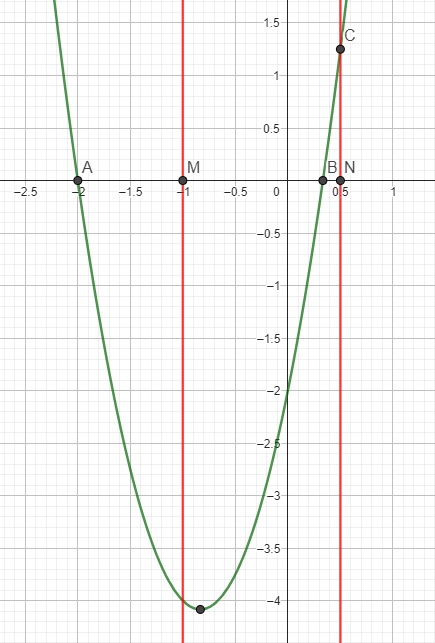
Cách làm đúng ở đây là cần sử dụng quy tắc tam thức bậc 2 (hoặc 1 số pp khác nhưng ko thể là hoành độ đỉnh). Lợi dụng quy tắc tam thức bậc 2: nếu pt bậc 2 có 2 nghiệm \(x_1;x_2\) thì \(a.f\left(x\right)< 0\) với \(x\in\left(x_1;x_2\right)\) và \(a.f\left(x\right)>0\) với \(x\notin\left(x_1;x_2\right)\).
Do đó để \(f\left(x\right)< 0\) ; \(\forall x\in\left(p;q\right)\) nào đó (khi a dương), đồng nghĩa khi đó p và q phải nằm giữa 2 nghiệm, hay \(f\left(p\right)\) và \(f\left(q\right)\) đều âm.
Hàm xác định trên khoảng đã cho khi và chỉ khi:
\(4\left(sin^6x+cos^6x\right)-6m.sin2x+2-m^2\ge0;\forall x\in\left(...\right)\)
\(\Leftrightarrow4\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]-6m.sin2x+2-m^2\ge0;\forall x\in...\)
\(\Leftrightarrow-3sin^22x-6m.sin2x-m^2+6\ge0\)
Đặt \(sin2x=t\Rightarrow t\in[-1;\dfrac{1}{2})\)
\(\Rightarrow f\left(t\right)=3t^2+6mt+m^2-6\le0\)
Theo định lý về dấu của tam thức bậc 2 thì điều này xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}f\left(-1\right)\le0\\f\left(\dfrac{1}{2}\right)< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-6m-3\le0\\m^2+3m-\dfrac{21}{4}< 0\end{matrix}\right.\)
Ủa biến đổi có sai ở đâu ko mà BPT cuối nhìn nghiệm xấu vậy

e/
\(y=5sinx+6cosx-7\)
\(=\sqrt{61}\left(\frac{5}{\sqrt{61}}sinx+\frac{6}{\sqrt{61}}cosx\right)-7\)
\(=\sqrt{61}\left(sinx.cosa+cosx.sina\right)-7\) (với \(a\in\left(0;\pi\right)\) sao cho \(cosa=\frac{5}{\sqrt{61}}\))
\(=\sqrt{61}.sin\left(x+a\right)-7\)
Do \(-1\le sin\left(x+a\right)\le1\Rightarrow7-\sqrt{61}\le y\le7+\sqrt{61}\)
\(y_{min}=7-\sqrt{61}\) khi \(sin\left(x+a\right)=-1\)
\(y_{max}=7+\sqrt{61}\) khi \(sin\left(x+a\right)=1\)
f/
\(y=2\left(\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx\right)+3\)
\(=2sin\left(x+\frac{\pi}{3}\right)+3\)
\(\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin\left(x+\frac{\pi}{3}\right)=-1\)
\(y_{max}=5\) khi \(x+\frac{\pi}{3}=1\)
c/
\(y=2\left(1-cos2x\right)+sin2x+cos2x\)
\(=sin2x-cos2x+2=\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)+2\)
Do \(-1\le sin\left(2x-\frac{\pi}{4}\right)\le1\)
\(\Rightarrow2-\sqrt{2}\le y\le2+\sqrt{2}\)
\(y_{min}=2-\sqrt{2}\) khi \(sin\left(2x-\frac{\pi}{4}\right)=-1\)
\(y_{max}=2+\sqrt{2}\) khi \(sin\left(2x+\frac{\pi}{4}\right)=1\)
d/
\(y=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-3sin^2x.cos^2x\)
\(=1-\frac{3}{4}sin^22x\)
Mà \(0\le sin^22x\le1\Rightarrow\frac{1}{4}\le y\le1\)
\(y_{min}=\frac{1}{4}\) khi \(sin^22x=1\)
\(y_{max}=1\) khi \(sin2x=0\)

Hàm xác định trên R khi và chỉ khi:
\(sin^4x+cos^4x+4sinx.cosx+m-5\ge0;\forall m\)
\(\Leftrightarrow sin^4x+cos^4x+4sinx.cosx-5\ge-m;\forall m\)
\(\Leftrightarrow-m\le\min\limits_{x\in R}f\left(x\right)\)
Với \(f\left(x\right)=sin^4x+cos^4x+4sinx.cosx-5\)
Ta có:
\(f\left(x\right)=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+4sinx.cosx-5\)
\(=-\dfrac{1}{2}\left(2sinx.cosx\right)^2+2sin2x-4\)
\(=-\dfrac{1}{2}sin^22x+2sin2x-4\)
\(=\dfrac{1}{2}\left(-sin^22x+4sin2x+5\right)-\dfrac{13}{2}\)
\(=\dfrac{1}{2}\left(5-sin2x\right)\left(sin2x+1\right)-\dfrac{13}{2}\ge-\dfrac{13}{2}\) do \(-1\le sin2x\le1\)
\(\Rightarrow\min\limits_{x\in R}f\left(x\right)=-\dfrac{13}{2}\Rightarrow m\ge\dfrac{13}{2}\)