Biết \(x\inℕ^∗\)và \(x,x+99\)là số chính phương. Tính tổng tất cả các giá trị của \(x.\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 9 2020
Đặt: \(t^2=x^2+x+6\)
=> \(4t^2=4x^2+4x+24=\left(2x+1\right)^2+23\)
=> \(4t^2-\left(2x+1\right)^2=23\)
<=> \(\left(2t-2x-1\right)\left(2t+2x+1\right)=23\)
Chia các trường hợp: => x và t
27 tháng 7 2018
xác định bé hơn x và lớn hơn x bao nhiêu rồi tính số số hạng rồi tính tổng
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$
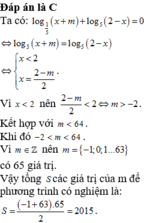
Có: x,x+99 là scp
thì bản chất x là scp rồi!
Đặt: \(x=a^2\)(a thuộc N*) Đặt vậy vì cho dù a âm đi nữa tìm x thì giá trị không đổi
Tới đây ta có:\(x^2+99=n^2\)
\(\Leftrightarrow\left(x-n\right)\left(x+n\right)=99\)
Chia TH giải ra x.
Sửa lại giúp mk: \(\left(n-x\right)\left(x+n\right)=99\)