Giúp mình bt này với mình đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(1.a.2Mg+O_2-^{t^o}\rightarrow2MgO\\ b.Fe+2AgNO_3\rightarrow Fe\left(NO_3\right)_2+2Ag\\ c.C_2H_4+3O_2-^{t^o}\rightarrow2CO_2+2H_2O\\ d.CuO+2HCl\rightarrow CuCl_2+H_2O\\ e.2Na+2H_2O\rightarrow2NaOH+H_2\\ f.4Al+3O_2-^{t^o}\rightarrow2Al_2O_3\)
\(2.a.Magie+Axitclohidric\rightarrow MagieClorua+Hidro\\ b.Mg+2HCl\rightarrow MgCl_2+H_2\\ c.m_{Mg}+m_{HCl}=m_{MgCl_2}+m_{H_2}\\ d.m_{HCl}=m_{MgCl_2}+m_{H_2}-m_{Mg}=47,5+1-12=36,5\left(g\right)\)

Phương trình tương đương
\(\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.,k\in Z\)
Xét họ nghiệm \(x=\dfrac{5\pi}{12}+k\pi,k\in Z\).
Do \(-\dfrac{\pi}{2}< \dfrac{5\pi}{12}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{11\pi}{12}< k\pi< \dfrac{9\pi}{4}\)
⇒ \(-\dfrac{11}{12}< k< \dfrac{9}{4}\). Mà k ∈ Z nên k ∈ {0 ; 1}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp :
S1 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12}\right\}\)
Xét họ nghiệm \(x=-\dfrac{\pi}{4}+k\pi\) với k ∈ Z.
Do \(-\dfrac{\pi}{2}< \dfrac{-\pi}{4}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{\pi}{4}< k\pi< \dfrac{35\pi}{12}\)
nên \(-\dfrac{1}{4}< k< \dfrac{35}{12}\). Mà k ∈ Z nên k∈ {0 ; 1 ; 2}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S2 = \(\left\{-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S = S1 \(\cup\) S2 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12};-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)


a: \(\widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Ta có: SA\(\perp\)(ABCD)
=>SA\(\perp\)AC
=>ΔSAC vuông tại A
Vì ABCD là hình vuông
nên \(AC=AD\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;\left(ABCD\right)}=60^0\)
b: Ta có: BD\(\perp\)AC
BD\(\perp\)SA
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SD}=\widehat{BSD}\)
Vì ABCD là hình vuông
nên \(AC=BD=a\sqrt{2}\)
ΔSAD vuông tại A
=>\(SA^2+AD^2=SD^2\)
=>\(SD^2=\left(a\sqrt{6}\right)^2+a^2=7a^2\)
=>\(SD=a\sqrt{7}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=a\sqrt{7}\)
Xét ΔSBD có \(cosBSD=\dfrac{SB^2+SD^2-BD^2}{2\cdot SB\cdot SD}\)
\(=\dfrac{7a^2+7a^2-2a^2}{2\cdot a\sqrt{7}\cdot a\sqrt{7}}=\dfrac{6}{7}\)
=>\(sinBSD=\sqrt{1-\left(\dfrac{6}{7}\right)^2}=\dfrac{\sqrt{13}}{7}\)
=>\(\widehat{BSD}\simeq31^0\)
=>\(\widehat{SB;\left(SAC\right)}\simeq31^0\)

1 plays
2 swimming
3 plays
4 painting
5 climbing
6 walking
7 because
8 take
9 favorite
10 easy

\(\left(x-3\right)^{30}=\left(x-3\right)^{10}\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=4\end{matrix}\right.\)
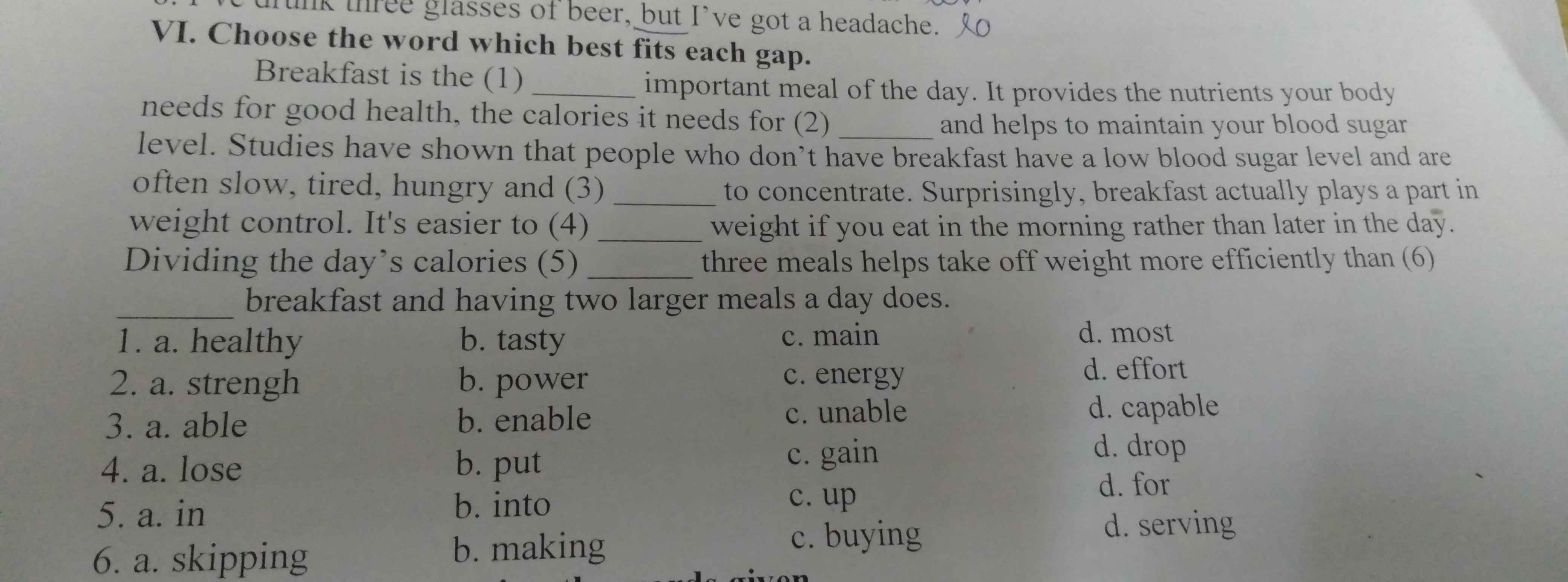
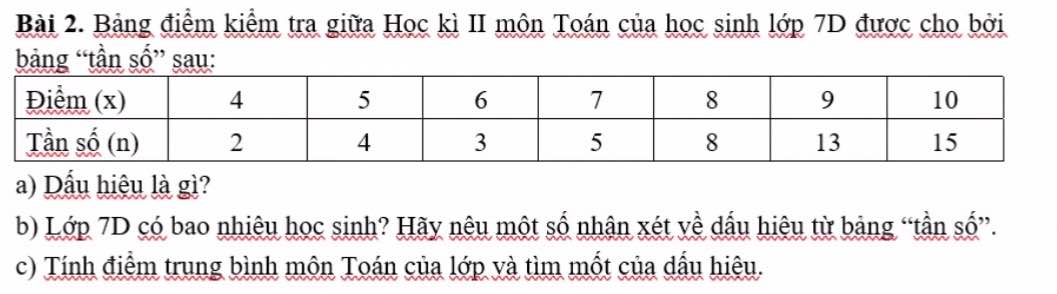







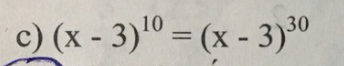 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp